Свойства плотности распределения
Для начала напомним, что такое плотность распределения:
Плотностью распределения $\varphi (x)$ непрерыной случайной величины называется первая производная от функции распределения вероятности $F(x)$.
Рассмотрим свойства плотности распределения:
Свойство 1: Функция $\varphi (x)$ плотности распределения неотрицательна:
Доказательство.
Мы знаем, что функция распределения $F(x)$ - неубывающая функция. Из определения следует, что $\varphi \left(x\right)=F'(x)$, а производная неубывающей функции -- есть функция неотрицательная.
ч. т. д.
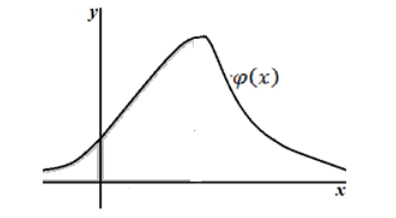
Геометрически это свойство означает, то график функции $\varphi \left(x\right)$ плотности распределения находится либо выше, либо на самой оси $Ox$ (рис. 1)
 неравенства $\varphi (x)\ge 0$.">
неравенства $\varphi (x)\ge 0$.">
Рисунок 1. Иллюстрация неравенства $\varphi (x)\ge 0$.
Свойство 2: Несобственный интеграл от функции плотности распределения пределах от $-\infty $ до $+\infty $ равен 1:
Доказательство.
Вспомним формулу для нахождения вероятности того, что случайная величина попадет интервал $(\alpha ,\beta )$:
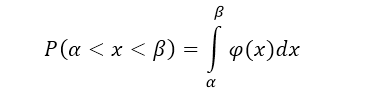
Рисунок 2.
Найдем вероятность того, что случайная величина попадет в интервал $(-\infty ,+\infty $):
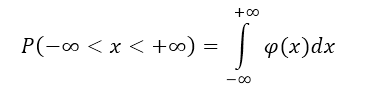
Рисунок 3.
Очевидно, что случайная величина всегда попадет в интервал $(-\infty ,+\infty $), следовательно, вероятность такого попадания равна единице. Получаем:
ч. т. д.
Геометрически, второе свойство означает, что площадь криволинейной трапеции, ограниченной графиком функции плотности распределения $\varphi (x)$ и осью абсцисс численно равна единице.
Можно также сформулировать обратное свойство:
Свойство 3: Любая неотрицательная функция $f(x)\ge 0$, удовлетворяющая равенству $\int\limits^{+\infty }_{-\infty }{f\left(x\right)dx}=1$ является функцией плотность распределения некоторой непрерывной случайной величины.
Вероятностный смысл плотности распределения
Придадим переменной $x$ приращение $\triangle x$.
Вероятностный смысл плотности распределения: Вероятность того, что непрерывная случайная величина $X$ примет значения из интервала$(x,x+\triangle x)$, приближенно равна произведению плотности распределения вероятности в точке $x$ на приращение $\triangle x$:
прямоугольника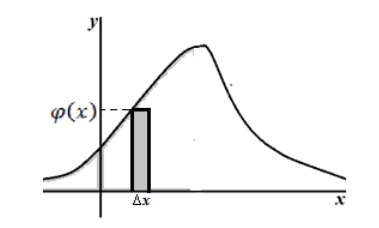
Рисунок 4. Геометрическая иллюстрация вероятностного смысла плотности распределения непрерывной случайной величины.
Примеры решения задач с использованием свойств плотности распределения
Функция плотности распределения вероятности имеет вид:
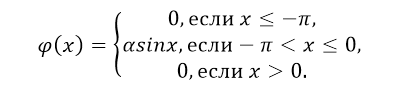
Рисунок 5.
- Найти коэффициент $\alpha $.
- Построить график плотности распределения.
Решение:
- Рассмотрим несобственный интеграл $\int\limits^{+\infty }_{-\infty }{\varphi \left(x\right)dx}$, получаем:
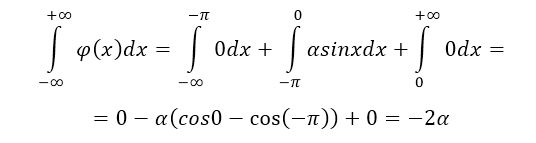
Рисунок 6.
Используя свойство 2, получим:
\[-2\alpha =1,\] \[\alpha =-\frac{1}{2}.\]То есть, функция плотности распределения имеет вид:
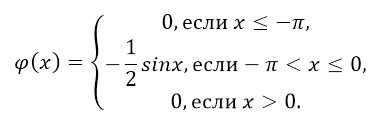
Рисунок 7.
- Построим её график:
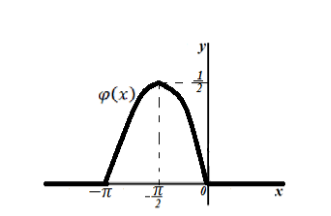
Рисунок 8.
Функция плотности распределения имеет вид $\varphi \left(x\right)=\frac{\alpha }{chx}$
(Напомним, что $chx$ -- гиперболический косинус).
Найти значение коэффициента $\alpha $.
Решение. Используем второе свойство:
\[\int\limits^{+\infty }_{-\infty }{\frac{\alpha }{chx}dx}=1,\] \[\alpha \int\limits^{+\infty }_{-\infty }{\frac{dx}{chx}}=1,\] \[\int\limits^{+\infty }_{-\infty }{\frac{dx}{chx}}={\mathop{lim}_{a\to -\infty } \int\limits^0_a{\frac{dx}{chx}}\ }+{\mathop{lim}_{b\to +\infty } \int\limits^b_0{\frac{dx}{chx}}\ }\]Так как $chx=\frac{e^x+e^{-x}}{2}$, то
\[\int{\frac{dx}{chx}}=2\int{\frac{dx}{e^x+e^{-x}}}=2\int{\frac{de^x}{{1+e}^{2x}}}=2arctge^x+C\]Тогда
\[\int\limits^{+\infty }_{-\infty }{\frac{dx}{chx}}={\mathop{lim}_{a\to -\infty } \left(-2arctge^a\right)\ }+{\mathop{lim}_{b\to +\infty } \left(2arctge^b\right)\ }=\pi \]Следовательно:
\[\pi \alpha =1,\] \[\alpha =\frac{1}{\pi }\]










