Действительная функция $\xi =\varphi (\omega )$ определенная на измеримом пространстве $\{ \Omega ,{\rm F}\} $ называется измеримой или случайной величиной, если
\[\forall B\subset B(R):{\rm \; \; }\{ \omega :{\rm \; \; }\varphi (\omega )\subset B\} \subset {\rm F}\]или
прообраз $f^{-1} (B)={\rm \; }\{ \omega :{\rm \; \; }\varphi (\omega )\subset B\} $
является измеримым множеством в $\Omega$.
Вероятностная мера $P_{\xi } $ на $\{ R,B(R)\} $ с вероятностью $P_{\xi } =P\{ \omega :{\rm \; \; }\varphi (\omega )\subset B\} $, $B\subset B(R)$, называется распределением вероятностей случайной величины $\xi$ на измеримом пространстве $\{ R,B(R)\} $.
Функция
\[F_{\xi } (x)=P(\omega :{\rm \; }\varphi (\omega ) это функция распределения случайной величины $\xi =\varphi (\omega )$.Свойства функции распределения:
- Функция распределения случайной величины определена на всей области $\forall x\in (-\infty ,+\infty )$.
- Функция распределения $F_{\xi } (x)$ -- неубывающая функция, то есть
- $\forall x_{1} ,x_{2} \in R$: $x_{1}
- Функция распределения $F_{\xi } (x)$ непрерывна слева в любой точке действительной оси, то есть \[\forall x_{0} \in R, \mathop{\lim }\limits_{x\to x_{0} -0} F_{\xi } (x)=F_{\xi } (x_{0} ).\]
- Функция распределения случайной величины имеет не более чем счетное число разрывов 1-го рода.
- $F_{\xi } (-\infty )=0$.
- $F_{\xi } (+\infty )=1$.
Всякая функция, которой подходят перечисленные свойства, называется функцией распределения некой случайной величины и наоборот.
Случайные величины обозначаются буквами греческого алфавита $\xi$, $\eta$, $\zeta$, $\dots$ .
Для применения функций распределения в инженерных и практических расчетах, обычно, случайные величины: дискретные и непрерывные, - рассматривают независимо.
Случайной величиной являются
- число выпавших очков на грани при подбрасывании игральной кости назовем дискретной случайной величиной;
- число выпадений герба при однократном подбрасывании монеты назовем дискретной случайной величиной;
- время безотказной работы телевизора назовем непрерывной случайной величиной;
- погрешности измерений назовем непрерывной случайной величиной.
Дискретной называется случайная величина, которая каждому элементарному событию $\omega$ ставит в соответствие одно из конечного или счетного набора
\[x_{1} ,x_{2} ,...,x_{n} , n\in N=\{ 1,2,3,...\} .\]Дискретная случайная величина полностью задается своим рядом распределения.
Пускай случайная величина $\xi$ принимает значения $x_{1}
Таблица, состоящая из двух строк называется рядом распределения (табл.1, 2)дискретной случайной величины если в верхней строке перечислены все возможные значения $x_{i} $ случайной величины, а в нижней -- вероятности $p_{i} =P(\xi =x_{i} )$ того, что случайная величина $\xi$ примет эти значения, причем $\sum \limits _{i}p_{i} =1$.
Таблица 1
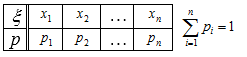
или
Таблица 2
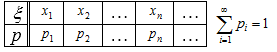
Графическим представлением ряда распределения является многоугольник распределения. Если на плоскости построить точки $(x_{i} ,p_{i} )$, $i=1,2,3,...,n$, и соединить их отрезками прямых, то полученная ломаная и называется многоугольником распределения дискретной случайной величины (рис. 1)
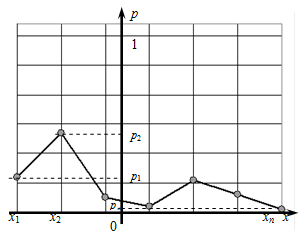
Для вычисления функции распределения дискретной случайной величины, имеем формулу
$F_{\xi } (x)=P(\xi
Непрерывные случайные величины
Непрерывная случайная величина это функцию $\xi =\varphi (\omega )$, множеством значений которой является некоторый числовой интервал $(a,b)$, $a,b\in R$, $a
Функция $\rho _{\xi } (x)$ - это плотность распределения вероятностей (или плотностью распределения) непрерывной случайной величины $\xi$, если она удовлетворяет условиям:
- $\forall x\in R$ $\rho _{\xi } (x)\ge 0$;
- $\int \limits _{-\infty }^{\infty }\rho _{\xi } (x) dx=1$.
Легко показать, что
\[F_{\xi } (x)=\int \limits _{-\infty }^{x}\rho _{\xi } (t) dt. \]Следствия свойств функции распределения
Некоторые полезные следствия свойств функции распределения случайной величины:
- $0\le F_{\xi } (x)\le 1$, $\forall x\in R$;
- $P(a\le \xi
- $P(a\le \xi
- $P(x\le \xi \le x+dx)=\rho _{\xi } (x)dx$;
- $P(\xi =x)=F_{\xi } (x+0)-F_{\xi } (x-0)$;
- $P(\xi \le x)=F_{\xi } (x+0)$.
Функция распределения это вероятность и следовательно безразмерна, а плотность, как следует из формулы:
\[\rho _{\xi } (x)=\frac{dF_{\xi } (x)}{dx} \]имеет размерность обратную времени. Кроме того, сравнивая законы дискретных и непрерывных случайных величин, легко заметить, что аналогом плотности является ряд распределения дискретной случайной величины.












