Описать случайную величину можно с используя закона распределения.
Законом распределения дискретной случайной величины называют соответствие между возможными значениями случайной величины и их вероятностями.
Закон распределения дискретной случайной величины $Х$ может быть задан в виде таблицы, в первой строке которой указаны все возможные значения случайной величины в порядке возрастания, а во второй строке соответствующие вероятности этих значений:
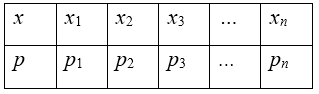
Рисунок 1.
где $р1+ р2+ ... + рn = 1$.
Даная таблица является рядом распределения дискретной случайной величины.
Если множество возможных значений случайной величины бесконечно, то ряд $р1+ р2+ ... + рn+ ...$ сходится и его сумма будет равна $1$.
Закон распределения дискретной случайной величины $Х$ можно представить графически, для чего в системе координат (прямоугольной) строят ломаную линию, которая последовательно соединяет точки с координатами $(xi;pi), i=1,2, ... n$. Линию, которую получили называют многоугольником распределения.
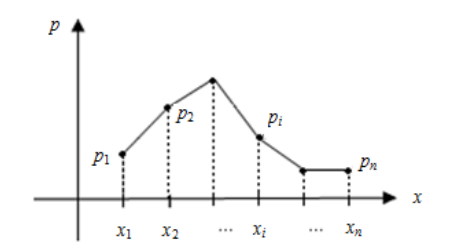
Рисунок 2.
Закон распределения дискретной случайной величины $Х$ может быть также представлен аналитически (с помощью формулы):
$P(X=xi)= \varphi (xi),i =1,2,3 ... n$.
Действия над дискретными вероятностями
При решении многих задач теории вероятности необходимо проводить операции умножения дискретной случайной величины на константу, сложения двух случайных величин, их умножения, поднесения к степени. В этих случаях необходимо придерживаться таких правил над случайными дискретными величинами:
Умножением дискретной случайной величины $X$ на константу $K$ называется дискретная случайная величина $Y=KX,$ которая обусловлена равенствами: $y_i=Kx_i,\ \ p\left(y_i\right)=p\left(x_i\right)=p_i,\ \ i=\overline{1,\ n}.$
Две случайные величины $x$ и $y$ называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приобрела вторая величина.
Суммой двух независимых дискретных случайных величин $X$ и $Y$ называют случайную величину $Z=X+Y,$ обусловлена равенствами: $z_{ij}=x_i+y_j$, $P\left(z_{ij}\right)=P\left(x_i\right)P\left(y_j\right)=p_ip'_j$, $i=\overline{1,n}$, $j=\overline{1,m}$, $P\left(x_i\right)=p_i$, $P\left(y_j\right)=p'_j$.
Умножением двух независимых дискретных случайных величин $X$ и $Y$ называют случайную величину $Z=XY,$ обусловлена равенствами: $z_{ij}=x_iy_j$, $P\left(z_{ij}\right)=P\left(x_i\right)P\left(y_j\right)=p_ip'_j$, $i=\overline{1,n}$, $j=\overline{1,m}$, $P\left(x_i\right)=p_i$, $P\left(y_j\right)=p'_j$.
Примем во внимание, что некоторые произведения $x_{i\ \ \ \ \ }y_j$ могут быть равными между собой. В таком случае вероятность сложения произведения равна сумме соответствующих вероятностей.
Например, если $x_2\ \ y_3=x_5\ \ y_7,\ $то вероятность $x_2y_3$ (или тоже самое $x_5y_7$) будет равна $p_2\cdot p'_3+p_5\cdot p'_7.$
Сказанное выше касается также и суммы. Если $x_1+\ y_2=x_4+\ \ y_6,$ то вероятность $x_1+\ y_2$ (или тоже самое $x_4+\ y_6$) будет равняться $p_1\cdot p'_2+p_4\cdot p'_6.$
Пусnm случайные величины $X$ и $Y$ заданы законами распределения:

Рисунок 3.
Где $p_1+p_2+p_3=1,\ \ \ p'_1+p'_2=1.$ Тогда закон распределения сумы $X+Y$ будет иметь вид
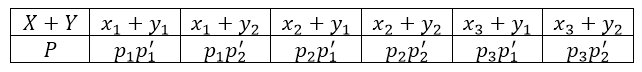
Рисунок 4.
А закон распределения произведения $XY$ будет иметь вид
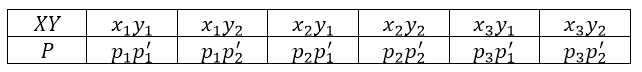
Рисунок 5.
Фунция распределения
Полное описание случайной величины дает также функция распределения.
Функцией распределения дискретной случайной величины $Х$ называется функция $F(x)$, которая определяет для каждого значения $х$ вероятность того, что случайная величина $Х$ примет значение, меньше $х$:
$F(x) = Р(Х$
Геометрически функция распределения разъясняется как вероятность того, что случайная величина $Х$ принимает значение, которое на числовой прямой изображается точкой, лежащей с левой стороны от точки $х$.
Свойства функции распределения
-
$0\le F\left(x\right)\le 1;$
-
$F\left(x\right)$$-$ функция неубывающая на промежутке ($- \infty $; $+ \infty $);
-
$F\left(x\right)$$-$ функция непрерывна слева в точках $х= xi (i=1,2,\dots n)$ и непрерывна во всех остальных точках;
$F\left(-\infty \right)=P \left(X
Если закон распределения дискретной случайной величины Х задан таблицей:
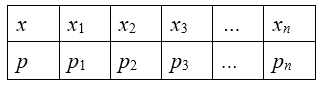
Рисунок 6.
то функция распределения $F(x)$ определяется за формулой:
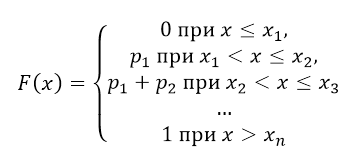
Рисунок 7.
Её график выглядит так:
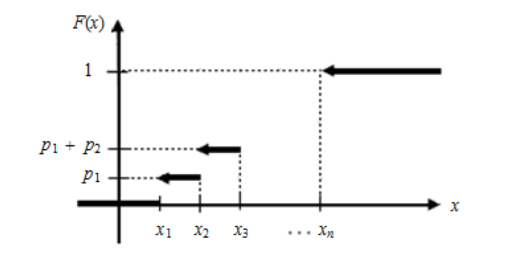
Рисунок 8.
Закон распределения дискретной случайной величины $\xi$ задано таблицей:
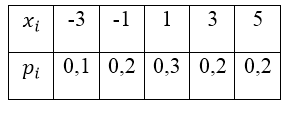
Рисунок 9.
Построить функцию распределения $F\left(x\right)$.
Если $x\le -3,$ то $F\left(x\right)=0;$
если $-3
если $-1
если $1
если $3
если $x>5,$ то $F\left(x\right)=0,8+0,2=1.$
Компактно $F\left(x\right)$ можно записать в такой форме:
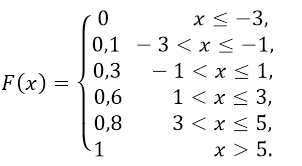
Рисунок 10.














