Понятие плотности распределения вероятностей непрерывной случайной величины
Пусть $X$ -- непрерывная случайная величина с функцией распределения вероятностей $F(x)$. Напомним определение функции распределения:
Функцией распределения называется функция $F(x)$ удовлетворяющая условию $F(x) = P(X⩽x)$.
Так как случайная величина является непрерывной, то, как нам уже известно, что функция распределения вероятностей F(x) будет непрерывной функцией. Пусть F(x) также дифференцируема на всей области определения.
Рассмотрим интервал (x,x+△x) (где △x - приращение величины x на нем).
Теперь устремляя значения приращения △x к нулю, получим:

Рисунок 1.
Таким образом, получаем:
Плотность распределения (плотность вероятности) φ(x) -- это производная функции распределения непрерывной случайной величины.
Плотность распределения, как и функция распределения, - это одна из форм закона распределения случайной величины. Однако закон распределения может быть записан через плотность распределения только для непрерывных случайных величин.
Геометрический смысл плотности распределения вероятностей непрерывной случайной величины
Кривая распределения -- это график функции φ(x) плотность распределения случайной величины (рис.2).

Рисунок 2. График плотности распределения. Автор24 — интернет-биржа студенческих работ
Геометрический смысл 1: Вероятность попадания непрерывной случайной величины в интервал (α,β) равна площади криволинейной трапеции, ограниченной графиком функции распределения φ(x) и прямыми x=α, x=β и y=0 (рис. 3).

Рисунок 3. Геометрическое изображение вероятности попадания непрерывной случайной величины в интервал (α, β). Автор24 — интернет-биржа студенческих работ
Геометрический смысл 2: Площадь бесконечной криволинейной трапеции, ограниченной графиком функции распределения φ(x), прямой y=0 и переменной прямой x есть ни что иное как функция распределения F(x) (рис. 4).

Рисунок 4. Геометрическое изображение функции вероятности F(x) через плотность распределения φ(x). Автор24 — интернет-биржа студенческих работ
Пусть функция распределения F(x) случайной величины X имеет следующий вид:

Рисунок 5.
- а) Найти значение α.
- б) Найти плотность распределения φ(x).
- в) Построить кривую распределения.
Решение:
а) Так как необходимо найти плотность распределения, то случайная величина X является непрерывной. Тогда, при x=2, получим, что $αx^2=1$, то есть 4α=1, α=1/4.
То есть:

Рисунок 6.
б) Так как:

Рисунок 7.
то получим:
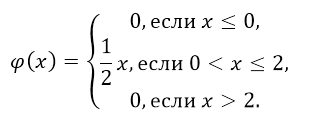
Рисунок 8.
в) Построим график функции φ(x).

Рисунок 9.














