Как нам уже известно, случайную величину можно задавать с помощью таблицы или с помощью функции распределения вероятности. Предположим теперь, что случайная величина $X$ является непрерывной, а функция распределения вероятности $F(x)$ непрерывна и дифференцируема в своей области определения. Тогда для такой случайной величины существует еще один способ её задания -- задания с помощью плотности распределения.
Плотностью распределения $\varphi (x)$ непрерыной случайной величины называется первая производная от функции распределения вероятности $F(x)$.
!!! Подчеркнем, что данное понятие не применимо к дискретной случайной величине.
Геометрически, плотность распределения связана с функцией распределения вероятностей следующим образом: площадь криволинейной трапеции, ограниченной графиком плотности распределения и находящейся по левую сторону от величины $x$ и есть функция распределения вероятности (рис. 1).
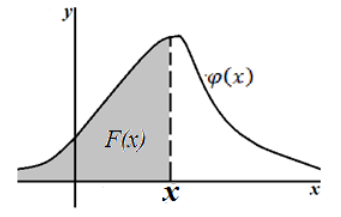
Рисунок 1. Связь функций $\varphi (x)$ и $F(x)$.
То есть:
Геометрический смысл: вероятность попадания непрерывной случайной величины в интервал $(\alpha ,\beta )$ равна площади криволинейной трапеции, ограниченной графиком функции распределения $\varphi \left(x\right)$ и прямыми $x=\alpha ,$ $x=\beta $ и $y=0$ (рис. 2).
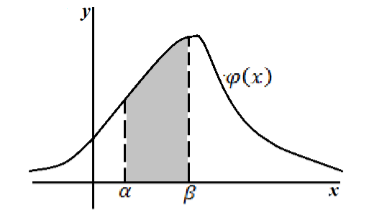
Рисунок 2. Геометрическое изображение вероятности попадания непрерывной случайной величины в интервал $(\alpha ,\beta )$.
Примеры задач на понятие плотности распределения
Пусть функция распределения $F(x)$ случайной величины $X$ имеет следующий вид:
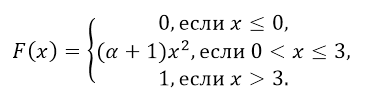
Рисунок 3.
а) Найти значение $\alpha $.
б) Найти плотность распределения $\varphi \left(x\right)$.
в) Построить график плотности распределения.
г) Найти вероятность попадания случайной величины в интервал $\left(1,2\right)$
Решение:
а) Так как необходимо найти плотность распределения, то случайная величина $X$ является непрерывной.
Тогда, при $x=3$, получим, что $(\alpha +1)x^2=1$, то есть
\[9\alpha +9=1,\] \[9\alpha =-8,\] \[\alpha =-\frac{8}{9}.\]То есть:
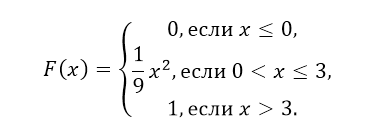
Рисунок 4.
б) Так как $\varphi (x)$ = $F'(x)$, то получим:
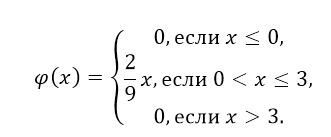
Рисунок 5.
в) Построим график функции $\varphi \left(x\right)$.
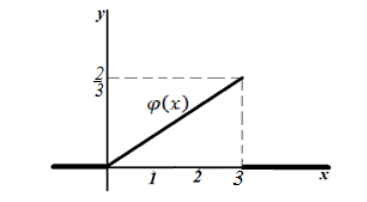
Рисунок 6.
г) Воспользовавшись геометрическим смыслом функции плотности распределения получим, что нам нужно найти площадь криволинейной трапеции, ограниченной функцией $y=\frac{2}{9}x$ и прямыми $x=1,$ $x=2$ и $y=0$.
Таким образом, получим:
\[P\left(1Найти функцию распределения непрерывной случайной величины и построить её график, если плотность распределения имеет вид:
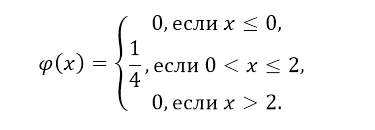
Рисунок 7.
Решение.
При решении будем использовать следующую формулу: $F\left(x\right)=\int\limits^x_{-\infty }{\varphi (x)dx}$
\begin{enumerate} \item При $x\le 0$, по формуле, получим:
\[F\left(x\right)=\int\limits^x_{-\infty }{\varphi (x)dx}=\int\limits^x_{-\infty }{0dx}=0\]\item При $0 \[F\left(x\right)=\int\limits^x_{-\infty }{\varphi (x)}=\int\limits^0_{-\infty }{0dx}+\int\limits^x_0{\frac{dx}{4}}=0+\frac{x}{4}-0=\frac{x}{4}\]
\item При $x>2$, по формуле, получим:
\[F\left(x\right)=\int\limits^x_{-\infty }{\varphi (x)}=\int\limits^0_{-\infty }{0dx}+\int\limits^2_0{\frac{dx}{4}}+\int\limits^x_2{0dx}=0+\frac{1}{2}-0+0=\frac{1}{2}\]\end{enumerate}
Таким образом, функция распределения имеет вид:
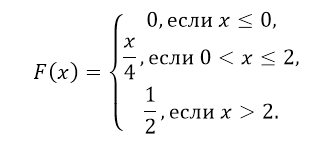
Рисунок 8.
Построим её график.
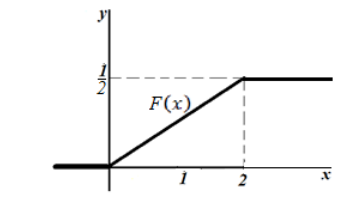
Рисунок 9.
!!! Заметим, что, так как дана плотность распределения, то случайная величина является непрерывной. Следовательно, функция $F(x)$ также должна быть непрерывной (как и получилось в нашем примере). Это может служить косвенной проверкой правильности решения такого рода задач.














