Напомним определение плотности вероятности.
Плотность распределения (плотность вероятности) $\varphi \left(x\right)$ -- это производная функции распределения непрерывной случайной величины.
Введем теперь понятие равномерного распределения вероятностей:
Распределение называется равномерным, если на интервале, содержащем все возможные значения случайной величины, плотность распределения постоянна, то есть:
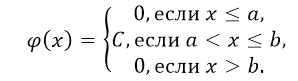
Рисунок 1.
Найдем значение константы $\ C$, используя следующее свойство плотности распределения: $\int\limits^{+\infty }_{-\infty }{\varphi \left(x\right)dx}=1$
Получим:
\[\int\limits^{+\infty }_{-\infty }{\varphi \left(x\right)dx}=\int\limits^a_{-\infty }{0dx}+\int\limits^b_a{Cdx}+\int\limits^{+\infty }_b{0dx}=0+Cb-Ca+0=C(b-a)\] \[C\left(b-a\right)=1\] \[C=\frac{1}{b-a}\]Таким образом, функция плотности равномерного распределения имеет вид:
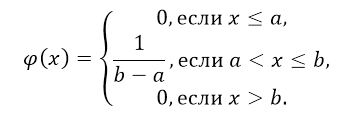
Рисунок 2.
График имеет следующий вид (рис. 1):
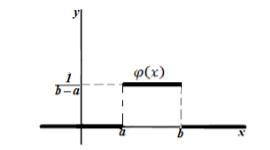
Рисунок 3. Плотность равномерного распределения вероятности
Функция равномерного распределения вероятностей
Найдем теперь функцию распределения при равномерном распределении.
Для этого будем использовать следующую формулу: $F\left(x\right)=\int\limits^x_{-\infty }{\varphi (x)dx}$
- При $x ≤ a$, по формуле, получим:
- При $a
- При $x> 2$, по формуле, получим:
Таким образом, функция распределения имеет вид:
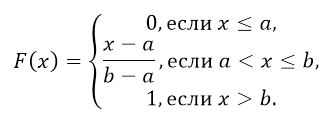
Рисунок 4.
График имеет следующий вид (рис. 2):
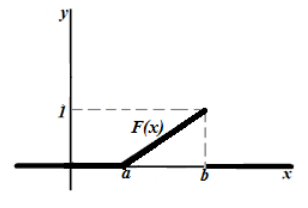
Рисунок 5. Функция равномерного распределения вероятности.
Вероятность попадания случайной величины в интервал $({\mathbf \alpha },{\mathbf \beta })$ при равномерном распределении вероятностей
Для нахождения вероятности попадания случайной величины в интервал $(\alpha ,\beta )$ при равномерном распределении вероятностей будем пользоваться следующей формулой:
Математическое ожидание:
Среднее квадратическое отклонение:
Примеры решения задачи на равномерное распределение вероятностей
Интервал движения между троллейбусами составляет 9 минут.
-
Составить функцию распределения и плотность распределения случайной величины $X$ ожидания пассажирами троллейбуса.
-
Найти вероятность того, что пассажир дождется троллейбус меньше чем через три минуты.
-
Найти вероятность того, что пассажир дождется троллейбус не менее чем через 4 минуты.
-
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение
Решение.
- Так как непрерывная случайная величина ожидания троллейбуса $X$ равномерно распределена, то $a=0,\ b=9$.
Таким образом, плотность распределения, по формуле функции плотности равномерного распределения вероятности, имеет вид:
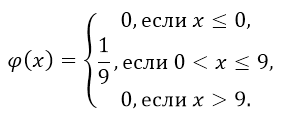
Рисунок 6.
По формуле функции равномерного распределения вероятности, нашем случае функция распределения имеет вид:
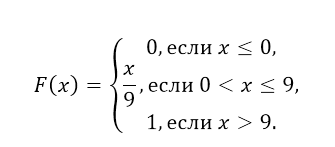
Рисунок 7.
- Данный вопрос можно переформулировать следующим образом: найдем вероятность попадания случайной величины равномерного распределения в интервал $\left(6,9\right).$
Получаем:
\[P\left(6Получаем: $P\left(0
- Математическое ожидание: $M\left(X\right)=\frac{a+b}{2}=\frac{9}{2}=4,5$.
Дисперсия: $D\left(X\right)=\frac{{(b-a)}^2}{12}=\frac{81}{12}=\frac{27}{4}$.
Среднее квадратическое отклонение: $\sigma \left(X\right)=\frac{b-a}{2\sqrt{3}}=\frac{9}{2\sqrt{3}}=\frac{3\sqrt{3}}{2}$












