Пусть нам задана функция плотности распределения непрерывной случайной величины. Тогда с её помощью мы можем найти вероятность того, что случайная величина попадет в интервал $(\alpha ,\beta )$.
Для начала вспомним несколько свойств функции распределения вероятности $F(x)$, которые понадобятся нам в дальнейшем.
Свойство 1: Для любых $X$ выполняется равенство:
Сформулируем и докажем следующую теорему:
Вероятность того, что непрерывная случайная величина $X$ примет значение из интервала $(\alpha ,\beta )$ равна значению определенного интеграла от $\alpha $ до $\beta $ плотности распределения $\varphi (x)$.
Доказательство.
Используя свойство 1, имеем:
\[P\left(\alpha \le XИспользуя формулу Ньютона-Лейбница, получим: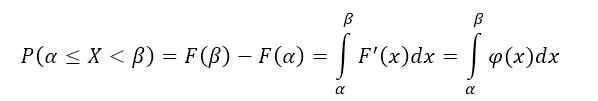
Рисунок 1.
Так как случайная величина $X$ непрерывна, то и функция распределения $F(x)$ также непрерывна. Следовательно, по свойству 2, получим:
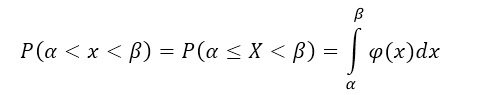
Рисунок 2.
ч. т. д.
Геометрически данную теорему можно интерпретировать следующим образом: Вероятность попадания случайной непрерывной величины $X$ в интервал $(\alpha ,\beta )$ равна площади криволинейной трапеции, ограниченной кривыми $y=\varphi \left(x\right),\ x=\alpha ,$ $x=\beta $ и $y=0$ (рис. 1).
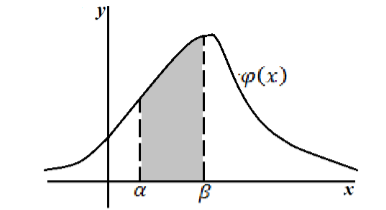
Рисунок 3. Геометрическое изображение вероятности попадания непрерывной случайной величины в интервал $(\alpha ,\beta )$.
Следствие 1: Если плотность распределения $\varphi (x)$ - четная функция, а значения $\alpha \ и\ \beta $ равны по абсолютной величине (по модулю), причем $\alpha \ne \beta $, то вероятность попадания непрерывной случайной величины в интервал $(\alpha ,\beta )$ можно найти по формуле:
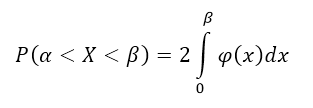
Рисунок 4.
Этот факт может быть легко показан геометрически:
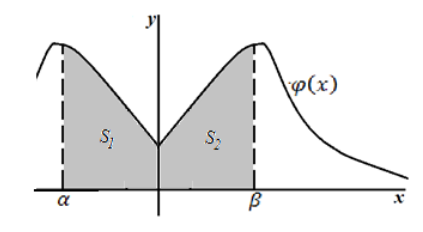
Рисунок 5.
Очевидно, что $S_1=S_2$.
Используя геометрический смысл плотности распределения, и получаем, что
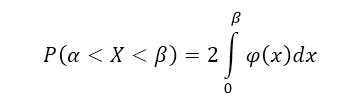
Рисунок 6.
Примеры задач на нахождение вероятности попадания непрерывной случайной величины в заданный интервал
Функция распределения имеет вид:
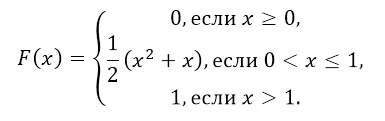
Рисунок 7.
Найти вероятности попадания случайной величины в интервал $(\frac{1}{4},\frac{1}{2})$.
Решение: Очевидно, что функция $F(x)$ непрерывна на сей области определения (в том числе непрерывна справа на всем интервале $(\frac{1}{4},\frac{1}{2})$). Значит по свойству 2, получим
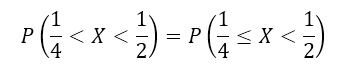
Рисунок 8.
Теперь, пользуясь свойством 1, получим:
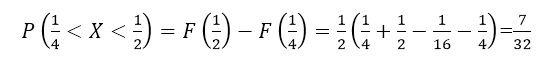
Рисунок 9.
Ответ: $\frac{7}{32}$.
Плотность распределения задана в виде:
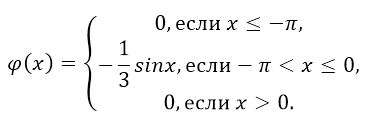
Рисунок 10.
Найти вероятности попадания случайной величины в интервал $(-\frac{\pi }{2},-\frac{\pi }{4})$.
Решение: Используя теорему 1, получим:
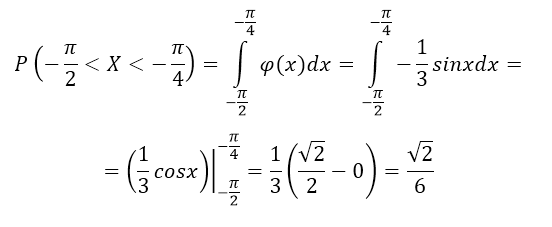
Рисунок 11.
Ответ: $\frac{\sqrt{2}}{6}$.
Функция плотности распределения имеет вид:
\[\varphi \left(x\right)=\frac{1}{4x^2+4}\]Построить график плотности распределения и найти вероятность попадания случайной величины в интервал $\left(-2,2\right).$
Решение: Построим график функции $\varphi \left(x\right)$:
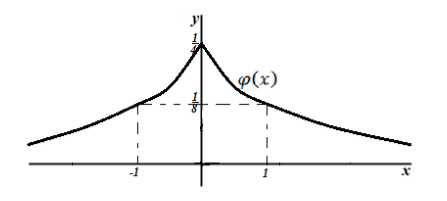
Рисунок 12.
Функция $\varphi \left(x\right)$ четна, концы интервала $\left(-2,2\right)$ симметричны относительно начала координат, следовательно, по следствию 1, получаем:
\[P\left(-2Ответ: $\frac{1}{2}arctg2.$











