Вписанная окружность
Если все стороны многоугольника являются касательными одной окружности, то такая окружность называется вписанной в многоугольник (рис 1).
Многоугольник, удовлетворяющий условию определения 1, называется описанным около окружности.
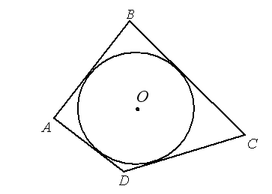
Рисунок 1. Вписанная окружность
Теорема 1 (об окружности, вписанной в треугольник)
В любой треугольник можно вписать окружность и притом только одну.
Доказательство.
Рассмотрим треугольник $ABC$. Проведем в нем биссектрисы, которые пересекаются в точке $O$ и проведем из нее перпендикуляры на стороны треугольника (Рис. 2)
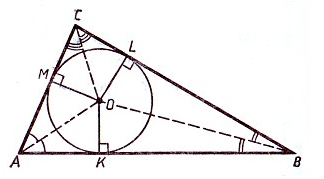
Рисунок 2. Иллюстрация теоремы 1
Существование: Проведем окружность с центром в точке $O$ и радиусом $OK.\ $Так как точка $O$ лежит на трех биссектрисах, то она равноудалена от сторон треугольника $ABC$. То есть $OM=OK=OL$. Следовательно, построенная окружность также проходит через точки $M\ и\ L$. Так как $OM,OK\ и\ OL$ - перпендикуляры к сторонам треугольника, то по теореме о касательной к окружности, построенная окружность касается всех трех сторон треугольника. Следовательно, в силу произвольности треугольника, в любой треугольник можно вписать окружность.
Единственность: Предположим, что в треугольник $ABC$ можно вписать еще одну окружность с центром в точке $O'$. Её центр равноудален от сторон треугольника, а, следовательно, совпадает с точкой $O$ и имеет радиус, равный длине $OK$. Но тогда эта окружность совпадет с первой.
Теорема доказана.
Следствие 1: Центр вписанной в треугольник окружности лежит в точке пересечения его биссектрис.
Приведем еще несколько фактов, связанных с понятием вписанной окружности:
-
Не во всякий четырехугольник можно вписать окружность.
-
В любом описанном четырехугольнике суммы противоположных сторон равны.
-
Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
Описанная окружность
Если на окружности лежат все вершины многоугольника, то окружность называется описанной около многоугольника (Рис. 3).
Многоугольник, удовлетворяющий условию определения 2, называется вписанным в окружность.
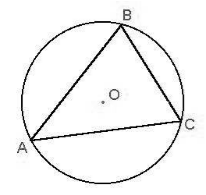
Рисунок 3. Описанная окружность
Теорема 2 (об окружности, описанной около треугольника)
Около любого треугольника можно описать окружность и притом только одну.
Доказательство.
Рассмотрим треугольник $ABC$. Проведем в нем серединные перпендикуляры, пересекающиеся в точке $O$, и соединим ее с вершинами треугольника (рис. 4)
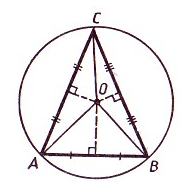
Рисунок 4. Иллюстрация теоремы 2
Существование: Построим окружность с центром в точке $O$ и радиусом $OC$. Точка $O$ равноудалена от вершин треугольника, то есть $OA=OB=OC$. Следовательно, построенная окружность проходит через все вершины данного треугольника, значит, она является описанной около этого треугольника.
Единственность: Предположим, что около треугольника $ABC$ можно описать еще одну окружность с центром в точке $O'$. Её центр равноудален от вершин треугольника, а, следовательно, совпадает с точкой $O$ и имеет радиус, равный длине $OC.$ Но тогда эта окружность совпадет с первой.
Теорема доказана.
Следствие 1: Центр описанной около треугольника окружности совпадает с точкой пересечения его серединных перпендикуляров.
Приведем еще несколько фактов, связанных с понятием описанной окружности:
-
Около четырехугольника не всегда можно описать окружность.
-
В любом вписанном четырехугольнике сумма противоположных углов равна ${180}^0$.
-
Если сумма противоположных углов четырехугольника равна ${180}^0$, то около него можно описать окружность.
Пример задачи на понятия вписанной и описанной окружности
В равнобедренном треугольнике основание равно 8 см, боковая сторона равна 5 см. Найти радиус вписанной окружности.
Решение.
Рассмотрим треугольник $ABC$. По следствию 1, мы знаем, что центр вписанной окружности лежит на пересечении биссектрис. Проведем биссектрисы $AK$ и $BM$, которые пересекаются в точке $O$. Проведем перпендикуляр $OH$ из точки $O$ на сторону $BC$. Изобразим рисунок:
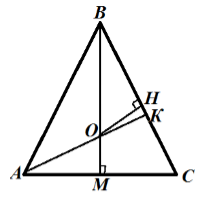
Рисунок 5.
Так как треугольник равнобедренный, то $BM$ и медиана и высота. По теореме Пифагора ${BM}^2={BC}^2-{MC}^2,\ BM=\sqrt{{BC}^2-\frac{{AC}^2}{4}}=\sqrt{25-16}=\sqrt{9}=3$. $OM=OH=r$ -- искомый радиус вписанной окружности. Так как $MC$ и $CH$ отрезки пересекающихся касательных, то по теореме о пересекающихся касательных, имеем $CH=MC=4\ см$. Следовательно, $BH=5-4=1\ см$. $BO=3-r$. Из треугольника $OHB$, по теореме Пифагора, получим:
\[{(3-r)}^2=r^2+1\] \[9-6r+r^2=r^2+1\] \[6r=8\] \[r=\frac{4}{3}\]Ответ: $\frac{4}{3}$.












