Теорема о площади треугольника
Площадь треугольника равна половине произведения двух сторон на синус угла между этими сторонами.
Доказательство.
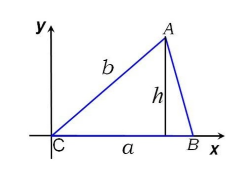
Пусть нам дан произвольный треугольник $ABC$. Обозначим длины сторон этого треугольника как $BC=a$, $AC=b$. Введем декартову систему координат, так, что точка $C=(0,0)$, точка $B$ лежит на правой полуоси $Ox$, а точка $A$ лежит в первой координатной четверти. Проведем высоту $h$ из точки $A$ (рис. 1).
 теоремы 1">
теоремы 1">
Рисунок 1. Иллюстрация теоремы 1
В этой системе координат, получаем, что
Высота $h$ равняется ординате точки $A$, следовательно
Тогда
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
Доказательство.
Пусть нам дан произвольный треугольник $ABC$. Обозначим длины сторон этого треугольника как $BC=a$, $AC=b,$ $AC=c$ (рис. 2).
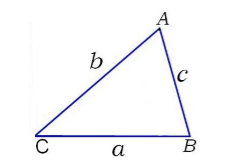
Рисунок 2.
Докажем, что
По теореме 1, имеем
Приравнивая их попарно, и получим, что
Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон треугольника без удвоенного произведения этих сторон на косинус угла между этими сторонами.
Доказательство.
Пусть нам дан произвольный треугольник $ABC$. Обозначим длины его сторон как $BC=a$, $AC=b,$ $AB=c$. Введем декартову систему координат, так, что точка $A=(0,0)$, точка $B$ лежит на положительной полуоси $Ox$, а точка $C$ лежит в первой координатной четверти (рис. 3).
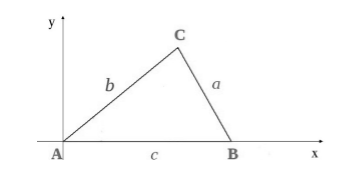
Рисунок 3.
Докажем, что
В этой системе координат, получаем, что
Найдем длину стороны $BC$ по формуле расстояния между точками
То есть
Пример задачи на использование данных теорем
Доказать, что диаметр описанной окружности произвольного треугольника равен отношению любой стороны треугольника к синусу противолежащего этой стороне угла.
Решение.
Пусть нам дан произвольный треугольник $ABC$. $R$ - радиус описанной окружности. Проведем диаметр $BD$ (Рис. 4).
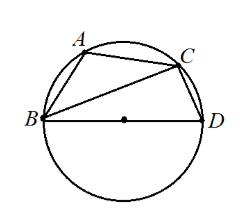
Рисунок 4.
Докажем, что $\frac{BC}{sinA}=2R$
Так как сторона $BD$ треугольника $DCB$ лежит на диаметре вписанной окружности, то он прямоугольный, следовательно, $sinD=\frac{BC}{BD}=\frac{BC}{2R}$.То есть
\[\frac{BC}{sinD}=2R\] \[\angle A={180}^0-\angle D\] \[sin\angle A={sin \left({180}^0-\angle D\right)\ }={sin \angle D\ }\]Следовательно,
\[\frac{BC}{sinA}=2R\]ч. т. д.
Найти третью сторону треугольника, если две его стороны равны 5 и 7, соответственно, а угол между ними равен ${60}^0.$
Решение.
Обозначим искомую сторону через $a$. Используя теорему 3, получим
\[a^2=25+49-70cos{60}^0=74-35=39\] \[a=\sqrt{39}\]Ответ: $\sqrt{39}$.

















