Одним из этапов исследования функции является нахождение экстремумов заданной функции, другими словами, максимума и минимума функции.
Некоторая точка называется точкой минимума заданной функции $y=f(x)$, если для всех точек из некоторой окрестности данной точки справедливо неравенство $f(x)\ge f(x_{0} )$, $x_{0} $ - точка минимума.
Некоторая точка называется точкой максимума заданной функции $y=f(x)$, если для всех точек из некоторой окрестности данной точки справедливо неравенство $f(x)\le f(x_{0} )$, $x_{0} $ - точка максимума.
Точки экстремума показаны на рис.
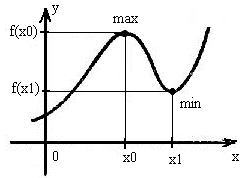
Рисунок 1.
Функция вида $y=ax^{2} +bx+c$ (парабола) имеет на области определения:
- минимум, если $a>0$;
- максимум, если $a
Экстремум параболы, рассматриваемой на всей области определения, совпадает с ее вершиной (рис.).
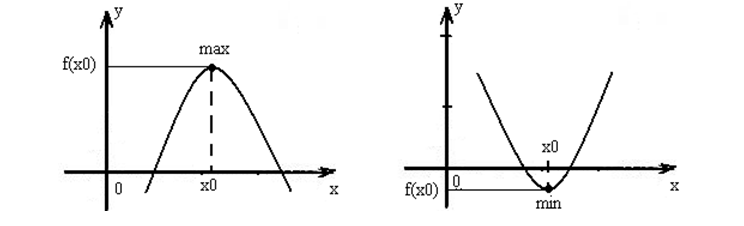
Рисунок 2.
Значения заданной функции в точках минимума и максимума называются соответственно минимумом и максимумом заданной функции.
Экстремумы функции делятся на:
- локальный экстремум;
- глобальный экстремум.
Определения 1 и 2 относятся к локальным экстремумам: локальный минимум и локальный максимум.
Наименьшее и наибольшее значения заданной функции на некотором промежутке являются глобальными экстремумами.
Глобальные экстремумы могут достигаться либо в точках локального экстремума, либо на концах отрезка.
Необходимое условие экстремума определяется следующей теоремой.
Если заданная функция $y=f(x)$ имеет экстремум в некоторой точке $x_{0} $, то ее производная $f'(x)$ в данной точке либо равна нулю, либо не существует.
Достаточные условия экстремума определяются следующими теоремами.
Первое условие.
Пусть для заданной функции $y=f(x)$ выполнены условия:
- данная функция $y=f(x)$непрерывна в окрестности точки $x_{0} $;
- $f'(x)$ при $x=x_{0} $ равна нулю или $f'(x)$ не существует;
- производная $f'(x)$ при переходе через данную точку $x_{0} $ меняет знак.
Тогда в точке $x=x_{0} $ заданная функция $y=f(x)$ имеет экстремум, причем он является минимумом, если при переходе через точку $x_{0} $ производная меняет знак с «-» на «+»; является минимумом, если при переходе через точку $x_{0} $ производная меняет знак с «+» на «-».
Второе условие.
Пусть для заданной функции $y=f(x)$ выполнены условия:
- данная функция $y=f(x)$непрерывна в окрестности точки $x_{0} $;
- $f'(x)$ при $x=x_{0} $ равна нулю;
- $f''(x)$ при $x=x_{0} $ не равна нулю.
Тогда в точке $x=x_{0} $ заданная функция $y=f(x)$ имеет экстремум, причем, если $f''(x)>0$ при $x=x_{0} $, то в данной точке заданная функция $y=f(x)$ имеет минимум; если $f''(x)
Если $f'(x)$ при переходе через точку $x_{0} $ не меняет свой знак, то в данной точке экстремума нет.
Алгоритм исследования заданной функции на экстремум включает следующие этапы:
- нахождение производной $f'(x)$;
- нахождение критических и стационарных точек, т.е. точек, в которых производная не существует или равна нулю;
- исследовать знак $f'(x)$на промежутках с помощью числовой прямой;
- определение экстремумов;
- нахождение значения заданной функции в точках экстремума.
Исследовать заданную функцию на минимум и максимум: $y=2x^{3} +12$.
Решение:
-
Найдем первую производную заданной функции: $y'=(2x^{3} +12)'=6x^{2} $.
-
Найдем критические и стационарные точки:
- Исследуем знак $f'(x)$ с помощью числовой прямой:
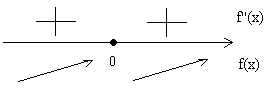
Рисунок 3.
- Так как производная заданной функции не меняет знак при переходе через критическую точку, то в данной точке нет ни максимума, ни минимума.
График заданной функции приведен на рис.
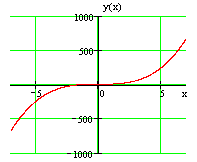
Рисунок 4.
Исследовать заданную функцию на минимум и максимум: $y=2x^{2} +12x$.
Решение:
-
Найдем первую производную заданной функции: $y'=(2x^{2} +12x)'=4x+12$.
-
Найдем критические и стационарные точки:
- Исследуем знак $f'(x)$ с помощью числовой прямой:

Рисунок 5.
-
$x=-3$ - точка минимума
-
$y(-3)=2\cdot (-3)^{2} +12\cdot (-3)=2\cdot 9-36=18-36=-18$
График заданной функции приведен на рис.
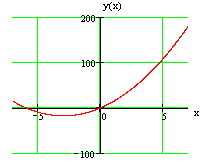
Рисунок 6.











