Понятие логарифмической функции
Для начала вспомним, что же вообще такое логарифм.
Логарифмом числа $b\in R$ по основанию $a$ ($a>0,\ a\ne 1$) называется число $c$, в которое нужно возвести число $a$, чтобы получить число $b$.
Рассмотрим показательную функцию $f\left(x\right)=a^x$, где $a >1$. Эта функция возрастает, непрерывна и отображает действительную ось на интервал $(0,+\infty )$. Тогда, по теореме о существовании обратной непрерывной функции, у нее в множестве $Y=(0,+\infty )$ существует обратная функция $x=f^{-1}(y)$, которая также непрерывна и возрастает в $Y$ и отображает интервал $(0,+\infty )$ на всю действительную ось. Эту обратную функцию называют логарифмической функцией по основанию $a\ (a >1)$ и обозначается $y={{log}_a x\ }$.
Теперь рассмотрим показательную функцию $f\left(x\right)=a^x$, где $0
Таким образом, мы определили логарифмическую функцию при всех возможных значениях основания $a$. Рассмотрим далее два этих случая отдельно.
Функция $y={{log}_a x\ },\ a >1$
Рассмотрим свойства данной функции.
-
Область определения -- интервал $(0,+\infty )$;
-
Область значения -- все действительные числа;
-
Функция не является ни четной, ни нечетной.
-
Точки пересечения с осями координат:
С осью $Oy$ пересечений нет.
При $y=0$, ${{log}_a x\ }=0,\ x=1.$ Пересечение с осью $Ox$: (1,0).
-
Функция положительна, при $x\in (1,+\infty )$ и отрицательна, при $x\in (0,1)$
-
$y'=\frac{1}{xlna}$;
-
Точки минимума и максимума:
\[\frac{1}{xlna}=0-корней\ нет\]Точек максимума и минимума нет.
-
Функция возрастает на всей области определения;
-
$y^{''}=-\frac{1}{x^2lna}$;
-
Промежутки выпуклости и вогнутости:
\[-\frac{1}{x^2lna}Функция выпукла на всей области определения; -
${\mathop{lim}_{x\to 0} y\ }=-\infty ,\ {\mathop{lim}_{x\to +\infty } y\ }=+\infty ,\ $;
-
График функции (Рис. 1).
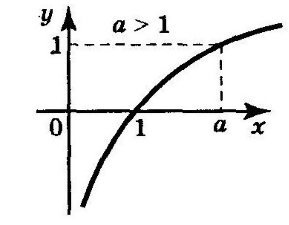
Рисунок 1. График функции $y={{log}_a x\ },\ a >1$
Функция $y={{log}_a x\ }, \ 0
Рассмотрим свойства данной функции.
-
Область определения -- интервал $(0,+\infty )$;
-
Область значения -- все действительные числа;
-
Функция не является ни четной, ни нечетной.
-
Точки пересечения с осями координат:
С осью $Oy$ пересечений нет.
При $y=0$, ${{log}_a x\ }=0,\ x=1.$ Пересечение с осью $Ox$: (1,0).
-
Функция положительна, при $x\in (0,1)$ и отрицательна, при $x\in (1,+\infty )$
-
$y'=\frac{1}{xlna}$;
-
Точки минимума и максимума:
\[\frac{1}{xlna}=0-корней\ нет\]Точек максимума и минимума нет.
-
Функция убывает на всей области определения;
-
$y^{''}=-\frac{1}{x^2lna}$;
-
Промежутки выпуклости и вогнутости:
\[-\frac{1}{x^2lna}>0\]Функция вогнута на всей области определения;
-
${\mathop{lim}_{x\to 0} y\ }=+\infty ,\ {\mathop{lim}_{x\to +\infty } y\ }=-\infty ,\ $;
-
График функции (Рис. 2).
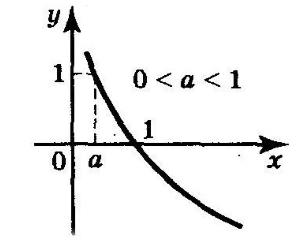
Примеры исследования и построения логарифмических функций
Исследовать и построить график функции $y=2-{{log}_2 x\ }$
-
Область определения -- интервал $(0,+\infty )$;
-
Область значения -- все действительные числа;
-
Функция не является ни четной, ни нечетной.
-
Точки пересечения с осями координат:
С осью $Oy$ пересечений нет.
При $y=0$, $2-{{log}_2 x\ }=0,\ x=4.$ Пересечение с осью $Ox$: (4,0).
-
Функция положительна, при $x\in (0,4)$ и отрицательна, при $x\in (4,+\infty )$
-
$y'=-\frac{1}{xln2}$;
-
Точки минимума и максимума:
\[-\frac{1}{xln2}=0-корней\ нет\]Точек максимума и минимума нет.
-
Функция убывает на всей области определения;
-
$y^{''}=\frac{1}{x^2ln2}$;
-
Промежутки выпуклости и вогнутости:
\[\frac{1}{x^2ln2} >0\]Функция вогнута на всей области определения;
-
${\mathop{lim}_{x\to 0} y\ }=+\infty ,\ {\mathop{lim}_{x\to +\infty } y\ }=-\infty ,\ $;
-
График функции:
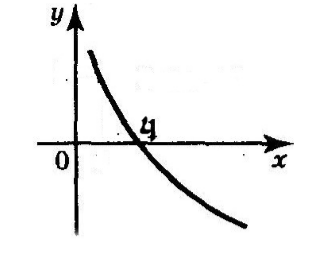
Рисунок 3.












