Проводить исследование заданной функции на минимум и максимум можно двумя способами:
- с помощью первой производной - $f'(x)$;
- с помощью второй производной - $f''(x)$.
Алгоритм исследования с помощью первой производной включает следующие этапы:
- нахождение первой производной заданной функции - $f'(x)$;
- нахождение критических точек ($f'(x)=0$ или не существует);
- исследование знака $f'(x)$ с помощью числовой прямой;
- определение характера критической точки;
- вычисление значения $f(x)$ при каждом критическом значении переменной.
Все возможные варианты, которые могут получиться в результате исследования, сведем в одну таблицу.
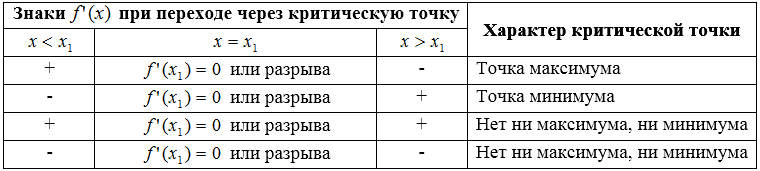
Рисунок 1.
Исследовать заданную функцию на минимум и максимум: $y=3x^{2} -5x$.
Решение:
-
Найдем первую производную заданной функции: $y'=(3x^{2} -5x)'=6x-5$.
-
Найдем критические точки:
- Исследуем знак $f'(x)$ с помощью числовой прямой:
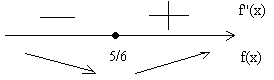
Рисунок 2.
-
Так как производная заданной функции меняет знак с «-» на «+», то имеем точку минимума.
-
Вычислим значение заданной функции в точке минимума:
График заданной функции приведен на рис.
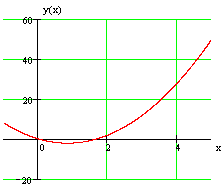
Рисунок 3.
Исследовать заданную функцию на минимум и максимум: $y=3x^{3} +2$.
Решение:
-
Найдем первую производную заданной функции: $y'=(3x^{3} +2)'=9x^{2} $.
-
Найдем критические точки:
- Исследуем знак $f'(x)$ с помощью числовой прямой:
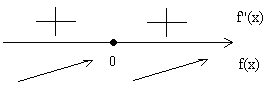
Рисунок 4.
- Так как производная заданной функции не меняет знак при переходе через критическую точку, то в данной точке нет ни максимума, ни минимума.
График заданной функции приведен на рис.
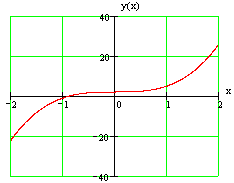
Рисунок 5.
Для исследования заданной функции на минимум и максимум с помощью второй производной необходимо пользоваться следующей теоремой.
Рассмотрим функцию $y=f(x)$. Пусть $x_{1} $ - критическая точка ($f'(x_{1} )=0$).
Тогда данная функция имеет максимум в критической точке $x=x_{1} $, если $f''(x_{1} )0$.
Если $f''(x_{1} )=0$ в критической точке $x=x_{1} $, то для данной функции $y=f(x)$ нельзя определить с помощью второй производной характер критической точки.
Алгоритм исследования с помощью первой производной включает следующие этапы:
- нахождение первой производной заданной функции - $f'(x)$;
- нахождение критических точек ($f'(x)=0$ или не существует);
- нахождение второй производной заданной функции - $f''(x)$;
- исследование знака $f''(x)$ в критической точке;
- определение характера критической точки;
- вычисление значения $f(x)$ при каждом критическом значении переменной.
Все возможные варианты, которые могут получиться в результате исследования, сведем в одну таблицу.

Рисунок 6.
Исследовать заданную функцию на минимум и максимум: $y=12x^{3} +4$.
Решение:
-
Найдем первую производную заданной функции: $y'=(12x^{3} +4)'=36x^{2} $.
-
Найдем критические точки:
-
Найдем вторую производную заданной функции: $y''=(36x^{2} )'=72x$.
-
Исследуем знак $f''(x)$ в критической точке: $y''(0)=72\cdot 0=0$
-
Так как вторая производная заданной функции обращается в ноль в критической точке, то мы не можем определить характер критической точки с ее помощью.
-
Для определения характера критической точки воспользуемся первой производной. Исследуем знак $f'(x)$ с помощью числовой прямой:
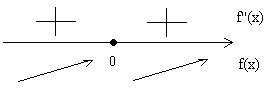
Рисунок 7.
- Так как производная заданной функции не меняет знак при переходе через критическую точку, то в данной точке нет ни максимума, ни минимума
График заданной функции приведен на рис.
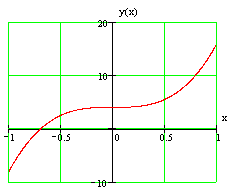
Рисунок 8.
Исследовать заданную функцию на минимум и максимум: $y=\cos x$.
Решение:
Поскольку заданная функция является периодической с периодом $2\pi $, то можно ограничиться исследованием функции на отрезке $[0;2\pi ]$.
-
Найдем первую производную заданной функции: $y'=(\cos x)'=-\sin x$.
-
Найдем критические точки:
-
Найдем вторую производную заданной функции: $y''=(-\sin x)'=-\cos x$.
-
Исследуем знак $f''(x)$ в критических точках:
Следовательно, в точках $x_{1} =0,x_{3} =2\pi $ имеем максимум данной функции, а в точке $x_{2} =\pi $ - минимум данной функции.
Вычислим значения заданной функции $f(x)$ при каждом критическом значении переменной:
График заданной функции приведен на рис.
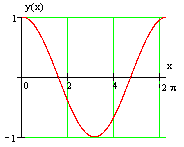
Рисунок 9.













