С понятием шара очень тесно связано понятие сферы, поэтому, вначале мы разберемся с этим понятием.
Понятие сферы
Сфера -- геометрическая фигура в пространстве, состоящая из всех точек, расположенных на равном расстоянии от заданной точки.
В рамках определения 1, заданная точка называется центром сферы.
Отрезок, соединяющий центр сферы с любой ее точкой называется радиусом сферы $(R)$ (Рис. 1).
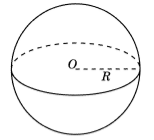
Рисунок 1.
Уравнение сферы
Выведем уравнение сферы в системе координат с тремя измерениями. Пусть центр сферы $C$ имеет координаты $(x_0,y_0,z_0)$, а радиус сферы равен $R$. Пусть точка $M$ с координатами $(x,y,z)$ -- произвольная точка этой сферы (рис. 2).
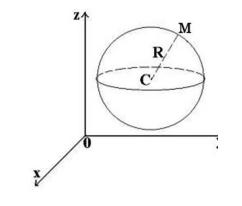
Рисунок 2.
Расстояние от центра сферы до точки $M$ вычисляется следующим образом
Но, так как $M$ лежит на окружности, то по определению 3, получаем $CM=R$. Тогда получим следующее
Уравнение (1) -- искомое нами уравнение.
Также можно выделить частный случай для уравнения сферы. Если центр сферы лежит вначале координат, то она имеет следующий вид уравнения:
Площадь сферы
Приведем формулу площади сферы, не вдаваясь в её вывод.
Площадь сферы определяется следующей формулой:
Шар
Шар -- геометрическая фигура, ограниченная какой либо сферой, включая саму сферу.
Выведем формулу объема шара.
Объем шара определяется следующей формулой
\[V=\frac{4}{3}\pi R^3\]Доказательство.
Пусть нам дан шар с радиусом, равным $R$. Проведем через центр сферы произвольно ось $Ox$ (рис. 3).
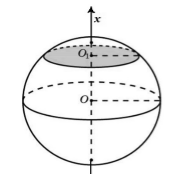
Рисунок 3.
Проведем через произвольную точку $O_1$ сечение, перпендикулярное оси $Ox.$ Данное сечение является окружностью. Обозначим ее радиус через $r$. Так как точка выбрана произвольно, то площадь окружности можно считать функцией от абсциссы $x$. Обозначим её через $S(x)$. Нам известно, что $S\left(x\right)=\pi r^2$. По теореме Пифагора, получим
То есть
Эта формула верна при всех $--R\le x\le R$
Вычисляя объем с помощью определенного интеграла, получим
Теорема доказана.
Пример задачи
Найти уравнение сферы у которой центр лежит в точке с координатами $(1,\ 1,0)$, а начало координат принадлежит этой сфере. Найти площадь данной сферы и объем шара, ограниченного данной сферой.
Решение.
Найдем сначала уравнение данной сферы. Для этого будем использовать формулу (1). Так как центр окружности лежит в точке $(1,\ 1,0)$, получим
\[{(x-1)}^2+{(y-1)}^2+z^2=r^2\]Найдем радиус окружности как расстояние от точки $(1,\ 1,0)$ до точки $(0,0,0)$
\[r=\sqrt{{(1-0)}^2+{(1-0)}^2}=\sqrt{2}\]Получаем, уравнение сферы имеет вид:
\[{(x-1)}^2+{(y-1)}^2+z^2=2\]Найдем площадь по формуле
\[S=4\pi R^2=8\pi \]По теореме 1, имеем
\[V=\frac{4}{3}\pi R^3=\frac{8\sqrt{2}}{3}\pi \]Ответ: ${(x-1)}^2+{(y-1)}^2+z^2=2$, $S=8\pi $, $V=\frac{8\sqrt{2}}{3}\pi $.












