Понятие объема
Понятие объема тел будем связывать с такой геометрической фигурой, как куб. За единицу объема фигуры будем принимать объем куба с ребром, равным единице. Из этого очевидно, что объем куба будет равняться кубу длины его ребра. Введем несколько свойств, для понятия объема геометрических фигур.
-
У равных геометрических тел равные объемы.
-
Тело, состоящее из нескольких тел, имеет своим объемом сумму объемов тел, из которых оно состоит.
Одной из основных формул для вычисления объемов тел является формула вычисления объема тел с помощью определенного интеграла:
Здесь $S\left(x\right)$ - функция площади сечения фигуры плоскостью, перпендикулярной оси $Ox$ (рис. 1).
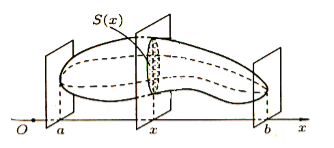
Рисунок 1.
Выведем теперь объемы фигур, хорошо известных в курсе стереометрии. Для это будем рассматривать поиск объемов как задачи на использование формулы нахождения объема с помощью интеграла.
Объем прямоугольного параллелепипеда
Доказать, что объем прямоугольного параллелепипеда определяется как произведение ширины, высоты и длины данного параллелепипеда.
Доказательство.
Обозначим высоту параллелепипеда через $c$, ширину через $b$ и длину через $a$. Выберем одну из вершин как начало координат и проведем ось $Ox$ через длину параллелепипеда (рис. 2.).
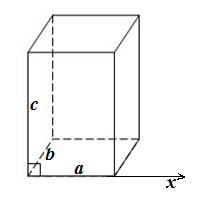
Рисунок 2.
Проводя сечения, перпендикулярно $Ox$ будем получать прямоугольники с площадью $S\left(x\right)=bc$. Используя формулу для вычисления объема тел, получим
\[V=\int\limits^a_0{bcdx}=bc{\left.x\right|}^a_0=bca-bc\cdot 0=abc\]ч. т. д.
Объем призмы
Доказать, что объем призмы определяется как произведение площади основания этой призмы на высоту.
Доказательство.
Рассмотрим произвольную призму, проведем в ней высоту и построим ось $Ox$ через эту высоту, считая началом координат точку $O$ основания высоты (рис. 3).
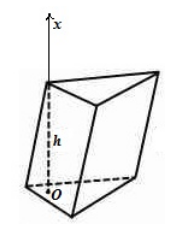
Рисунок 3.
Проводя сечения, перпендикулярно $Ox$ будем получать многоугольники с $S\left(x\right)=S_{осн}$. Используя формулу для вычисления объема тел, получим
\[V=\int\limits^h_0{S_{осн}dx}=S_{осн}{\left.x\right|}^h_0=S_{осн}h-S_{осн}\cdot 0=S_{осн}h\]ч. т. д.
Объем цилиндра
Доказать, что объем цилиндра определяется как произведение площади основания цилиндра на его высоту.
Рассмотрим произвольный цилиндр, проведем в нем высоту и построим ось $Ox$ через эту высоту, считая началом координат точку $O$ основания высоты (рис. 4).
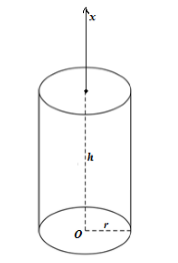
Рисунок 4.
Проводя сечения, перпендикулярно $Ox$ будем получать окружности с $S\left(x\right)=\pi r^2$. Используя формулу для вычисления объема тел, получим
\[V=\int\limits^h_0{\pi r^2dx}=\pi r^2{\left.x\right|}^h_0=\pi r^2h-\pi r^2\cdot 0=S_{осн}h\]ч. т. д.
Объем шара
Доказать, что объем шара определяется следующей формулой
\[V=\frac{4}{3}\pi R^3\]Доказательство.
Пусть нам дан шар с радиусом, равным $R$. Проведем через центр сферы произвольно ось $Ox$ (рис. 5).
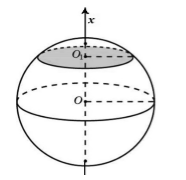
Рисунок 5.
Проведем через произвольную точку $O_1$ сечение, перпендикулярное оси $Ox.$ Данное сечение является окружностью. Обозначим ее радиус через $r$. Так как точка выбрана произвольно, то площадь окружности можно считать функцией от абсциссы $x$. Обозначим её через $S(x)$. Нам известно, что $S\left(x\right)=\pi r^2$. По теореме Пифагора, получим
\[r=\sqrt{R^2-x^2}\]То есть
\[S\left(x\right)=\pi (R^2-x^2)\]Эта формула верна при всех $--R\le x\le R$
Вычисляя объем с помощью определенного интеграла, получим
\[V=\int\limits^R_{-R}{\pi (R^2-x^2)}=\frac{4}{3}\pi R^3\]ч. т. д.












