
Предмет стереометрии
Стереометрия - один из разделов геометрии, в котором изучаются пространственные фигуры и их свойства. Слово стереометрия образовано из двух греческих слов $\sigma $$\tau $$\varepsilon $$\rho $$\varepsilon $$o$$\varsigma $ -- «объемный» и $\mu $$\varepsilon $$\tau $$\rho $$\varepsilon$$\omega $ -- «измерять».
Основными объектами изучения в стереометрии являются геометрические тела и поверхности.
Геометрическое тело -- это фигура в пространстве, которая является ограниченной, связной и содержит все свои граничные точки.
Граница геометрического тела называется поверхностью этого геометрического тела.
Основными объектами изучения являются многогранники и поверхности вращения.
Многогранником называется геометрическое тело в пространстве, которое ограниченно несколькими многоугольниками.
Примерами многогранников могут быть тетраэдр, куб, октаэдр, додекаэдр, икосаэдр и другие (рис. 1).
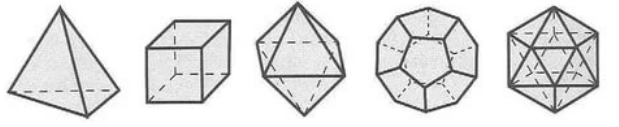
Рисунок 1. Примеры многогранников
Поверхность, которая образуется путем вращения какой-либо произвольной линии вокруг прямой, называется поверхностью вращения.
При этом, прямая, вокруг которой вращается поверхность, называется осью вращения и является осью симметрии для полученной поверхности.
Примерами поверхностей вращения могут быть цилиндр, конус, шар и другие (рис. 2).
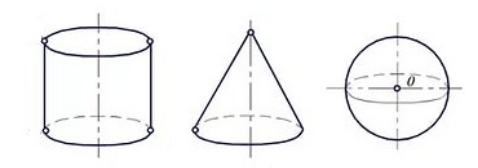
Рисунок 2. Примеры поверхностей вращения
Аксиомы стереометрии
Основными и неопределяемыми объектами в стереометрии являются точка, прямая и плоскость. Приведем теперь аксиомы стереометрии. Они делятся на
Первая группа аксиом -- аксиомы о взаимном расположении точек, прямых и плоскостей в пространстве.
-
Каждая прямая и плоскость содержит в себе какие-либо точки.
-
Можно найти как минимум три точки, которые не принадлежат одной прямой и как минимум четыре точки, которые не принадлежат одной плоскости.
-
Через любые две точки можно построить единственную прямую.
-
Через любые три точки можно построить единственную плоскость.
-
Если плоскости принадлежат две точки какой-либо прямой, то вся эта прямая лежит в данной плоскости.
-
Если точка принадлежит двум различным плоскостям, то эти плоскости имею общую прямую, которой принадлежат все их общие точки.
-
Для любых двух точек прямой, существует третья точка прямой, лежащая между первыми двумя.
-
Любую прямую можно разделить на два луча точкой $A$, лежащей на этой прямой. При этом точки, лежащие на одном луче, находятся с одной стороны от точки $A$, а точки, лежащие на разных лучах -- по разные стороны от точки $A$.
-
Любую плоскость можно разделить на две полуплоскости прямой $a$, лежащей в этой плоскости. При этом, точки, лежащие в одной полуплоскости находятся с одной стороны от прямой $a$, а точки, лежащие в разных полуплоскостях -- по разные стороны от прямой $a$.
-
Любое пространство можно разделить на два полупространства плоскостью $\alpha $, принадлежащей в этому пространству. При этом, точки, лежащие в одном полупространстве находятся с одной стороны от плоскости $\alpha $, а точки, лежащие в разных полупространствах -- по разные стороны от плоскости $\alpha $.
Вторая группа аксиом связана с равенством фигур.
-
Если при наложении концы одного отрезка отображаются на концы другого отрезка, то эти отрезки совпадут.
-
От начала любого луча можно отложить единственный равный какому-либо отрезку отрезок.
-
В полуплоскость всегда можно отложить единственный неразвернутый угол, равный какому-либо неразвернутому углу, от любого луча этой плоскости.
-
Любая фигура при наложении совпадает сама с собой.
-
Равенство фигур обладает свойством симметричности.
-
Равенство фигур обладает свойство транзитивности.
Третья группа аксиом связана с измерением отрезков.
-
Длина любого отрезка -- положительное действительное число.
-
Для любого действительного положительного числа существует отрезок, имеющий такую длину.
Последняя аксиома - аксиома параллельности.
- Через точку, не лежащую на прямой, можно провести единственную параллельную данной прямой прямую в любой плоскости пространства.
Примеры задач
Рассмотрим две задачи на использование аксиом стереометрии, которые считаются следствиями из этих аксиом.
Докажите, что через прямую и точку, не принадлежащую ей можно провести единственную плоскость.
Доказательство.
Рассмотрим рисунок 3.
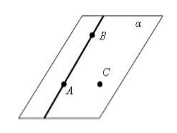
Рисунок 3.
Возьмем две произвольные точки $A\ и\ B$ на данной прямой. Так как точки $A,B$ и $C$ не лежат на одной прямой, то по аксиоме 4 через них можно провести единственную плоскость $\alpha $. Так как точки $A\ и\ B$ принадлежат и прямой, и плоскости $\alpha $, то данная прямая содержится в плоскости $\alpha .$
ч. т. д.
Докажите, что через две пересекающиеся прямые можно провести единственную плоскость.
Доказательство.
Рассмотрим рисунок 4.
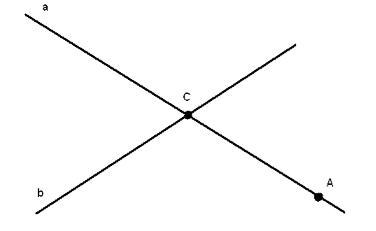
Рисунок 4.
Пусть прямые пересекаются в точке $C$. Построим точку $A$ на прямой $a$, отличную от $C$. Используя задачу 1, мы можем провести единственную плоскость $\alpha $ через прямую $b$ и точку $A$. Так как плоскость $\alpha $ содержит в себе две точки прямой $a$, то по аксиоме 5 она содержит всю эту прямую.
ч. т. д.











