Деление на число и деление заданных комплексных чисел выполняются для чисел, представленных в любой форме записи.
Делением заданного комплексного числа $z=a+b\cdot i$ на некоторое действительное число $k\ne 0$ является комплексное число, которое определяется равенством
Выполнить деление заданных комплексных чисел на число $k=\sqrt{3} $:
1) $z_{1} =\sqrt{3} +\sqrt{3} \cdot i$; 2) $z_{2} =5-4\cdot i$; 3) $z_{3} =\sqrt{3} \cdot i$.
Решение:
Для деления заданных комплексных чисел на действительное число воспользуемся определением и получим:
1) $\frac{z_{1} }{k} =\frac{z_{1} }{\sqrt{3} } =\frac{\sqrt{3} +\sqrt{3} \cdot i}{\sqrt{3} } =\frac{\sqrt{3} }{\sqrt{3} } +\frac{\sqrt{3} }{\sqrt{3} } \cdot i=1+1\cdot i$;
2) $\frac{z_{2} }{k} =\frac{z_{2} }{\sqrt{3} } =\frac{5-4\cdot i}{\sqrt{3} } =\frac{5}{\sqrt{3} } -\frac{4}{\sqrt{3} } \cdot i$;
3) $\frac{z_{3} }{k} =\frac{z_{3} }{\sqrt{3} } =\frac{0+\sqrt{3} \cdot i}{\sqrt{3} } =\frac{0}{\sqrt{3} } +\frac{\sqrt{3} }{\sqrt{3} } \cdot i=0+1\cdot i=i$.
При делении заданного комплексного числа $z=a+b\cdot i$ на действительное число $k\, \, (|k|>1)$ модуль этого числа уменьшается в $|k|$ раз:
При умножении заданного комплексного числа $z=a+b\cdot i$ на действительное число $k\, \, (|k|
Графическая интерпретация операции деления заданного комплексного числа $z=a+b\cdot i$ на число $k\, \, (|k|>1)$: длина радиус-вектора, изображающего исходное комплексное число, уменьшается в $|k|$ раз (радиус-вектор становится короче в $|k|$ раз).
Графическая интерпретация операции умножения заданного комплексного числа $z=a+b\cdot i$ на число $k\, \, (|k|
Иллюстрация примера деления заданного комплексного числа $z=a+b\cdot i$ на число $k_{1} =2,\, \, k_{2} =\frac{1}{4} $ с использованием комплексной плоскости приведена на рис.1-2.
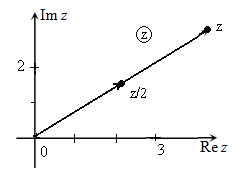
Рис. 1
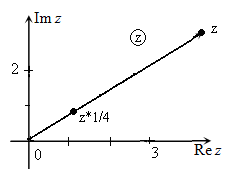
Рис. 2
Частным двух заданных комплексных чисел в тригонометрической форме представления $z_{1} =r_{1} \cdot (\cos \varphi _{1} +i\sin \varphi _{1} )$ и $z_{2} =r_{2} \cdot (\cos \varphi _{2} +i\sin \varphi _{2} )$ ($r_{2} \ne 0$) является комплексное число, которое определяется равенством
Выполнить деление заданных комплексных чисел:
1) $z_{1} =\sqrt{3} \cdot (\cos \frac{\pi }{4} +i\cdot \sin \frac{\pi }{4} )$ и $z_{2} =2\cdot (\cos \frac{2\pi }{3} +i\cdot \sin \frac{2\pi }{3} )$; 2) $z_{1} =4\cdot (\cos \pi +i\cdot \sin \pi )$ и $z_{2} =5\cdot (\cos \frac{\pi }{2} +i\cdot \sin \frac{\pi }{2} )$.
Решение:
Для деления заданных комплексных чисел воспользуемся определением и получим:
1)Частным двух заданных комплексных чисел $z_{1} =a_{1} +b_{1} i$ и $z_{2} =a_{2} +b_{2} i$ ($r_{2} =\sqrt{a_{2}^{2} +b_{2}^{2} } \ne 0)$ является комплексное число, которое определяется равенством
Равенство, указанное в определении 3, достаточно сложно для запоминания, поэтому на практике при делении заданных комплексных чисел, представленных в алгебраической форме, используют алгоритм, который описан в примечании 5.
Чтобы выполнить операцию деления заданных комплексных чисел, представленных в алгебраической форме необходимо:
- представить запись операции деления в виде дроби;
- числитель дроби и знаменатель дроби умножить на число сопряженное знаменателю;
- привести полученное выражение к алгебраической записи.
Выполнить деление комплексных чисел:
1) $z_{1} =3+i$ и $z_{2} =2-i$; 2) $z_{1} =3+2i$ и $z_{2} =1+2i$.Решение:
Для деления комплексных чисел воспользуемся алгоритмом, приведенным в примечании 5, и получим:
1)Частным двух заданных комплексных чисел в показательной форме $z_{1} =r_{1} \cdot e^{i\varphi _{1} } $ и $z_{2} =r_{2} \cdot e^{i\varphi _{2} } $ является комплексное число, которое определяется равенством
Выполнить деление комплексных чисел:
1) $z_{1} =\sqrt{3} \cdot e^{i\cdot \frac{\pi }{4} } $ и $z_{2} =2\cdot e^{i\cdot \frac{\pi }{3} } $; 2) $z_{1} =\sqrt{5} \cdot e^{i\cdot \frac{2\pi }{3} } $ и $z_{2} =2\cdot e^{i\cdot \frac{\pi }{2} } $.Решение:
Для деления комплексных чисел воспользуемся определением и получим:
1)










