Выражение вида $z=a+bi$, где $a$ и $b$ - вещественные числа, а $i$ - «мнимая единица», называется комплексным числом $z$. Мнимая единица определяется равенством $i=\sqrt{-1} $ или $i^{2} =-1$.
Комплексное число вида $\overline{z}=a-bi$ называется числом комплексно-сопряженным для $z=a+bi$.
Записать комплексно-сопряженные числа для заданных комплексных чисел:
1) $z_{1} =2+10i$; 2) $z_{2} =4$; 3) $z_{3} =-5i$
Решение:
Для комплексного числа $z=a+bi$ комплексно-сопряженным будет являться число $\overline{z}=a-bi$.
Для числа $z_{1} =2+10i$ получим $\overline{z_{1} }=2-10i$.
Для числа $z_{2} =4$ получим $\overline{z_{2} }=4$.
Для числа $z_{3} =-5i$ получим $\overline{z_{3} }=5i$.
Комплексная плоскость
Любое комплексное число можно изобразить на плоскости, которую принято называть комплексной плоскостью. Комплексная плоскость аналогична прямоугольной декартовой системе координат, исключение составляют только названия осей:
Комплексно-сопряженное число $\overline{z}=a-bi$ изображается на комплексной плоскости точкой, симметричной относительно действительной оси, для точки, изображающей некоторое комплексное число $z=a+bi$.
Изобразить на комплексной плоскости числа $z_{1} =3+2i,\, \, z_{2} =-2,\, \, \, z_{3} =i$ и комплексно-сопряженные к ним.
Решение:
Для комплексного числа $z=a+bi$ комплексно-сопряженным будет являться число $\overline{z}=a-bi$.
Для числа $z_{1} =3+2i$ получим $\overline{z_{1} }=3-2i$.
Для числа $z_{2} =-2$ получим $\overline{z_{2} }=-2$.
Для числа $z_{3} =i$ получим $\overline{z_{3} }=-i$.
Отмечая соответствующие точки на плоскости, получим изображение комплексных чисел (рис.1)
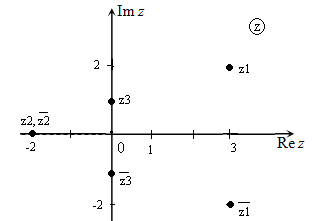
Рис. 1
Если комплексное число изображается точкой на вещественной оси, то комплексно-сопряженное число изображается той же самой точкой.
Два комплексных числа $z_{1} $ и $z_{2} $ можно сравнить между собой.
Некоторые комплексные числа $z_{1} =a_{1} +b_{1} i$ и $z_{2} =a_{2} +b_{2} i$ называются равными, если выполняются следующие равенства $a_{1} =a_{2} ,b_{1} =b_{2} $. Обозначение: $z_{1} =z_{2} $.
Некоторое комплексное число $z_{1} =a_{1} +b_{1} i$ равно нулю тогда и только тогда, когда $a_{1} =0,b_{1} =0$.
Сравнить заданные комплексные числа: 1) $z_{1} =3+2i$ и $z_{2} =3+2i$; 2) $z_{1} =3+3i$ и $z_{2} =3-2i$.
Решение:
1) Для чисел $z_{1} =3+2i$ и $z_{2} =3+2i$ имеем $3=3,\, \, \, 2=2$, следовательно, $z_{1} =z_{2} $.
2) Для чисел $z_{1} =3+3i$ и $z_{2} =3-2i$ имеем $3=3,\, \, \, 2\ne -2$, следовательно, $z_{1} \ne z_{2} $.
Выделяют три формы представления (записи) комплексных чисел:
- алгебраическая;
- тригонометрическая;
- показательная.
Алгебраическая форма записи
Запись некоторого комплексного числа $z$ в виде $z=a+bi$ называется алгебраической формой записи (или алгебраической записью) комплексного числа. При этом:
- $a$ - вещественная (действительная) часть, обозначение $Rez=a$;
- $b$ - мнимая часть, обозначение $Imz=b$.
Тригонометрическая форма записи
Запись комплексного числа $z$ в виде $z=r\cdot (\cos \varphi +i\sin \varphi )$ называется тригонометрической формой записи, где число $r$ - модуль комплексного числа $z$, определяемый по формуле $r=|z|=|a+bi|=\sqrt{a^{2} +b^{2} } $, $\varphi $ - аргумент комплексного числа $z$, определяемый по формуле $\varphi =arctg \frac{b}{a} $.
Показательная форма записи
Запись комплексного числа $z$ в виде $z=r\cdot e^{i\varphi } $ называется показательной формой записи, где число $r$ - модуль комплексного числа $z$, определяемый по формуле $r=|z|=|a+bi|=\sqrt{a^{2} +b^{2} } $, $\varphi $ - аргумент комплексного числа $z$, определяемый по формуле $\varphi =arctg\frac{b}{a} $.
Привести примеры комплексных чисел, представленных в различных формах записи.
Решение:
Алгебраическая запись: $z_{1} =\sqrt{3} +(-\sqrt{2} )\cdot i$, $z_{2} =3+2i$.
Тригонометрическая запись: $z=\sqrt{3} \cdot (\cos 2\pi +i\cdot \sin 2\pi )$.
Показательная запись: $z=3\cdot e^{i\cdot \pi } $.
Операции над комплексными числами
Над комплексными числами можно выполнять следующие действия: сложение, вычитание, умножение, деление, возведение в степень, извлечение корня.
Операции сложения и вычитания выполняются для чисел, представленных в алгебраической форме.
Умножение, деление и возведение в степень выполняются для чисел, представленных в любой форме записи.
Извлечение корня выполняется для чисел, представленных в тригонометрической форме.
Сумма
Суммой двух заданных комплексных чисел $z_{1} =a_{1} +b_{1} i$ и $z_{2} =a_{2} +b_{2} i$ является комплексное число, которое определяется равенством $z_{1} +z_{2} =(a_{1} +b_{1} i)+(a_{2} +b_{2} i)=(a_{1} +a_{2} )+(b_{1} +b_{2}$.
Разность
Разностью двух заданных комплексных чисел $z_{1} =a_{1} +b_{1} i$ и $z_{2} =a_{2} +b_{2} i$ является комплексное число, которое определяется равенством $z_{1} -z_{2} =(a_{1} +b_{1} i)-(a_{2} +b_{2} i)=(a_{1} -a_{2} )+(b_{1} -b_{2}$.
Выполнить действия: 1) $z_{1} +z_{2} $2) $z_{1} -z_{2} $ для комплексных чисел $z_{1} =3+3i$ и $z_{2} =3-2i$.
Решение:
1) $z_{1} +z_{2} =(3+3i)+(3-2i)=(3+3)+(3-2)i=6+i$
2) $z_{1} +z_{2} =(3+3i)-(3-2i)=(3-3)-(3+2)i=0-5i=-5i$
Произведение
Произведением двух заданных комплексных чисел $z_{1} =a_{1} +b_{1} i$ и $z_{2} =a_{2} +b_{2} i$ является комплексное число, которое получается перемножением данных чисел по правилам алгебры с учетом того, что $i^{2} =-1$.
Произведением двух заданных комплексных чисел $z_{1} =r_{1} \cdot (\cos \varphi _{1} +i\sin \varphi _{1} )$ и $z_{2} =r_{2} \cdot (\cos \varphi _{2} +i\sin \varphi {2} )$ является комплексное число, которое определяется равенством $z_{1} \cdot z_{2} =r_{1} \cdot r_{2} \cdot [\cos (\varphi _{1} +\varphi _{2} )+i\sin (\varphi _{1} +\varphi _{2})$.
Выполнить умножение комплексных чисел:
$z_{1} =3+3i$ и $z_{2} =3-2i$; 2) $z_{1} =\sqrt{3} \cdot (\cos 2\pi +i\cdot \sin 2\pi )$ и $z_{2} =\sqrt{3} \cdot (\cos \pi +i\cdot \sin \pi )$.
Решение:
1) $z_{1} \cdot z_{2} =(3+3i)\cdot (3-2i)=3\cdot 3+3\cdot 3i+3\cdot (-2i)+3i\cdot (-2i)$
$=9+9i-6i-6i^{2} =9+3i+6=15+3i $
2)$z_{1} \cdot z_{2} =\left(\sqrt{3} \cdot (\cos 2\pi +i\cdot \sin 2\pi )\right)\cdot \left(\sqrt{3} \cdot (\cos \pi +i\cdot \sin \pi )\right)=$ $=\sqrt{3} \cdot \sqrt{3} \cdot [\cos (2\pi +\pi )+i\cdot \sin (2\pi +\pi )]3\cdot (\cos 3\pi +i\cdot \sin 3\pi ) $
Частное
Частным двух заданных комплексных чисел $z_{1} =r_{1} \cdot (\cos \varphi _{1} +i\sin \varphi _{1} )$ и $z_{2} =r_{2} \cdot (\cos \varphi _{2} +i\sin \varphi _{2} )$ является комплексное число, которое определяется равенством $z_{1} \cdot z_{2} =\frac{r_{1} }{r_{2} } \cdot [\cos (\varphi _{1} -\varphi _{2} )+i\sin (\varphi _{1} -\varphi _{2})$.
Чтобы выполнить операцию деления комплексных чисел, представленных в алгебраической форме необходимо:
- представить запись операции деления в виде дроби;
- числитель и знаменатель дроби умножить на число сопряженное знаменателю;
- привести полученное выражение к алгебраической записи.
Выполнить деление комплексных чисел:
1) $z_{1} =3+i$ и $z_{2} =2-i$; 2) $z_{1} =2\cdot (\cos 2\pi +i\cdot \sin 2\pi )$ и $z_{2} =4\cdot (\cos \pi +i\cdot \sin \pi )$.
Решение:
1)$\frac{z_{1} }{z_{2} } =\frac{3+i}{2-i} =\frac{(3+i)(2+i)}{(2-i)(2+i)} =\frac{6+2i+3i+i^{2} }{2^{2} -i^{2} } =\frac{6+5i-1}{4+1} =\frac{5+5i}{5} =1+i$
2)$z_{1} \cdot z_{2} =\left(2\cdot (\cos 2\pi +i\cdot \sin 2\pi )\right)\div \left(4\cdot (\cos \pi +i\cdot \sin \pi )\right)=$
$=2\cdot 4\cdot [\cos (2\pi -\pi )+i\cdot \sin (2\pi -\pi )]=8\cdot (\cos \pi +i\cdot \sin \pi )$
Степень
Степенью порядка $n$ комплексного числа $z=r\cdot (\cos \varphi +i\sin \varphi )$ является комплексное число, которое определяется равенством $z^{n} =r^{n} \cdot (\cos n\varphi +i\sin n\varphi _{1} )$.
Данная формула называется формулой Муавра.
Выполнить действие $z^{4} $, где $z=2\cdot (\cos \pi +i\cdot \sin \pi )$.
Решение:
По формуле Муавра получим:
$z^{4} =2^{4} \cdot (\cos 4\pi +i\cdot \sin 4\pi )=16\cdot (\cos 4\pi +i\cdot \sin 4\pi).$
Корень
Корнем $n$-й степени комплексного числа $z=r\cdot (\cos \varphi +i\sin \varphi )$ является комплексное число, которое определяется равенством $\sqrt[{n}]{z} =\sqrt[{n}]{r} \cdot (\cos \frac{\varphi +2\pi k}{n} +i\sin \frac{\varphi +2\pi k}{n} ),\, \, \, k=0..n-1$.
Выполнить действие $\sqrt[{3}]{z} $, где $z=2\cdot (\cos \pi +i\cdot \sin \pi )$.
Решение:
Для $k=0$ получаем: $w_{1} =\sqrt[{3}]{z} =\sqrt[{3}]{2} \cdot \left(\cos \frac{\pi }{3} +i\cdot \sin \frac{\pi }{3} \right)$.
Для $k=1$ получаем: $w_{2} =\sqrt[{3}]{z} =\sqrt[{3}]{2} \cdot \left(\cos \frac{\pi +2\pi }{3} +i\cdot \sin \frac{\pi +2\pi }{3} \right)=\sqrt[{3}]{2} \cdot \left (\cos \pi +i\cdot \sin \pi \right)$.
Для получаем: Для $k=2$ получаем: $w_{3} =\sqrt[{3}]{z} =\sqrt[{3}]{2} \cdot \left(\cos \frac{\pi +4\pi }{3} +i\cdot \sin \frac{\pi +4\pi }{3} \right)=\sqrt[{3}]{2} \cdot \left(\cos \frac{5\pi }{3} +i\cdot \sin \frac{5\pi }{3} \right)$














