Выражение вида $z=a+bi$, где $a$ и $b$ - вещественные числа, а $i$ - «мнимая единица», называется комплексным числом $z$. Мнимая единица определяется равенством $i=\sqrt{-1} $ или $i^{2} =-1$.
Запись некоторого комплексного числа $z$ в виде $z=a+bi$ называется алгебраической формой записи (или алгебраической записью) комплексного числа. При этом:
- $a$ - вещественная (действительная) часть, обозначение $Rez=a$;
- $b$ - мнимая часть, обозначение $Imz=b$.
Выписать действительную и мнимую части для заданных комплексных чисел:
1) $z_{1} =5\sqrt{2} +3i$; 2) $z_{2} =13$; 3) $z_{3} =-3\sqrt{5} \cdot i$; 4) $z_{4} =3\sqrt{2} -6i$
Решение:
Для комплексного числа $z=a+bi$ $Rez=a$, $Imz=b$.
Для числа $z_{1} =5\sqrt{2} +3i$ имеем $Rez=5\sqrt{2} ,Imz=3$.
Для числа $z_{2} =13$ имеем $Rez=13,Imz=0$.
Для числа $z_{3} =-3\sqrt{5} \cdot i$ имеем $Rez=0,Imz=-3\sqrt{5} $.
Для числа $z_{4} =3\sqrt{2} -6i$ имеем $Rez=3\sqrt{2} ,Imz=-6$.
Комплексная плоскость
Любое комплексное число можно изобразить на плоскости, которую принято называть комплексной плоскостью. Комплексная плоскость аналогична прямоугольной декартовой системе координат, исключение составляют только названия осей:
Любому заданному комплексному числу $z$ можно поставить в соответствие точку комплексной плоскости, координатами которой являются числа $a$ и $b$ - $(a,b)$ (числа $Rez$ и $Imz$ - $(Rez;Imz)$).
Любой заданной точке $(x,y)$ плоскости можно поставить в соответствие комплексное число $z=x+yi$ ($Rez=x$,$Imz=y$).
Зная действительную и мнимую части комплексного числа, записать данное число:
1) $Rez=\sqrt{3}$,$Imz=1$; 2) $Rez=8$,$Imz=0$; 3) $Rez=0$,$Imz=-\sqrt{3}$ ; 4) $Rez=3$,$Imz=6$
Решение:
Для $Rez=a$, $Imz=b$ соответствует запись комплексного числа $z=a+bi$ ($z=Rez+Imz\cdot i$).
Для числа $Rez=\sqrt{3} ,Imz=1$ имеем $z_{1} =\sqrt{3} +1\cdot i$.
Для числа $Rez=8,Imz=0$ имеем $z_{2} =8+0\cdot i=8$.
Для числа $Rez=0,Imz=-\sqrt{3} $ имеем $z_{3} =0-\sqrt{3} \cdot i=-\sqrt{3} \cdot i$.
Для числа $Rez=3,Imz=6$ имеем $z_{4} =3+6\cdot i$.
Зная действительную и мнимую части комплексного числа, изобразить данное число на комплексной плоскости:
1) $Rez=3,Imz=0$; 2) $Rez=0,Imz=2$; 3) $Rez=3,Imz=2$; 4) $Rez=-2,Imz=1$.
Решение:
Изобразим на комплексной плоскости числа, соответствующие записи $Rez=x,Imz=y$.
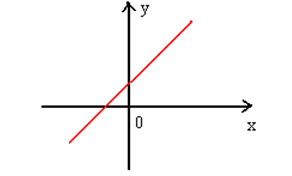
Рис. 2
Комплексное число вида $\overline{z}=a-bi$ называется числом комплексно-сопряженным для $z=a+bi$.
Записать комплексно-сопряженные числа для заданных комплексных чисел:
1) $z_{1} =\sqrt{2} +5i$; 2) $z_{2} =3$; 3) $z_{3} =-\sqrt{5} \cdot i$; 4) $z_{4} =3\sqrt{2} -15i$
Решение:
Для комплексного числа $z=a+bi$ комплексно-сопряженным будет являться число $\overline{z}=a-bi$.
Для числа $z_{1} =\sqrt{2} +5i$ имеем $a=\sqrt{2} ,b=5$, следовательно, получим $\overline{z_{1} }=\sqrt{2} -5i$.
Для числа $z_{2} =3$ имеем $a=3,b=0$, следовательно, получим $\overline{z_{2} }=3$.
Для числа $z_{3} =-\sqrt{5} i$ имеем $a=0,b=-\sqrt{5} $, следовательно, получим $\overline{z_{3} }=\sqrt{5} i$.
Для числа $z_{4} =3\sqrt{2} -15i$ имеем $a=3\sqrt{2} ,b=-15$, следовательно, получим $\overline{z_{4} }=3\sqrt{2} +15i$.
Комплексно-сопряженное число $\overline{z}=a-bi$ изображается на комплексной плоскости точкой, симметричной относительно действительной оси, для точки, изображающей некоторое комплексное число $z=a+bi$.
Изобразить на комплексной плоскости числа $z_{1} =3+i,\, \, z_{2} =-2,\, \, \, z_{3} =i,z_{4} =-2-2i$ и комплексно-сопряженные к ним.
Решение:
Для комплексного числа $z=a+bi$ комплексно-сопряженным будет являться число $\overline{z}=a-bi$.
Для числа $z_{1} =3+i$ получим $\overline{z_{1} }=3-i$.
Для числа $z_{2} =-2$ получим $\overline{z_{2} }=-2$.
Для числа $z_{3} =i$ получим $\overline{z_{3} }=-i$.
Для числа $z_{4} =-2-2i$ получим $\overline{z_{4} }=-2+2i$.
Значение действительной части откладывается по оси $Rez$, а мнимой части -- по оси $Imz$.
Отмечая соответствующие точки на плоскости, получим изображение комплексных чисел (рис.3)
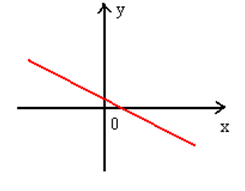
Рис. 3
Если комплексное число изображается точкой на вещественной оси, то комплексно-сопряженное число изображается той же самой точкой.
Изобразить на комплексной плоскости числа комплексно-сопряженные к отмеченным.
Решение:
Значение действительной части откладывается по оси $Rez$, а мнимой части -- по оси $Imz$.
Изображая комплексно-сопряженные числа на комплексной плоскости, воспользуемся примечаниями 1 и 2.
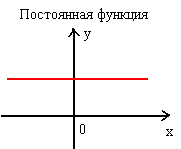
Рис. 4