Умножение комплексных чисел

Источник статьи

Автор24 — учеба по твоим правилам

Умножение на число и умножение заданных комплексных чисел выполняются для чисел, представленных в любой форме записи.

Определение 1

Произведением заданного комплексного числа $z=a+b\cdot i$ на действительное число $k$ является комплексное число, которое определяется равенством \[k\cdot z=k\cdot (a+b\cdot i)=k\cdot a+k\cdot b\cdot i.\]

Пример 1

Выполнить умножение комплексных чисел на число $k=\sqrt{3} $:

1) $z_{1} =\sqrt{3} +\sqrt{3} \cdot i$; 2) $z_{2} =5-4\cdot i$; 3) $z_{3} =\sqrt{3} \cdot i$.

Решение:

Для умножения комплексных чисел на число воспользуемся определением и получим:

1) $k\cdot z_{1} =\sqrt{3} \cdot z_{1} =\sqrt{3} \cdot \left(\sqrt{3} +\sqrt{3} \cdot i\right)=\sqrt{3} \cdot \sqrt{3} +\sqrt{3} \cdot \sqrt{3} \cdot i=3+3\cdot i$;

2) $k\cdot z_{2} =\sqrt{3} \cdot z_{2} =\sqrt{3} \cdot (5-4\cdot i)=\sqrt{3} \cdot 5-\sqrt{3} \cdot 4\cdot i=5\sqrt{3} -4\sqrt{3} \cdot i$;

3) $k\cdot z_{3} =\sqrt{3} \cdot z_{3} =\sqrt{3} \cdot (0+\sqrt{3} \cdot i)=\sqrt{3} \cdot \sqrt{3} \cdot i=3i$.

Примечание 1

При умножении заданного комплексного числа $z=a+b\cdot i$ на число $k\, \, (|k|>1)$ модуль этого числа увеличивается в $|k|$ раз:

\[|k\cdot z|=|k|\cdot \sqrt{a^{2} +b^{2} } .\]

Примечание 2

При умножении заданного комплексного числа $z=a+b\cdot i$ на число $k\, \, (|k|

\[|k\cdot z|=\frac{\sqrt{a^{2} +b^{2} } }{\left|\frac{1}{k} \right|} .\]

Примечание 3

Графическая интерпретация операции умножения заданного комплексного числа $z=a+b\cdot i$ на число $k\, \, (|k|>1)$: длина радиус-вектора, изображающего исходное комплексное число, увеличивается в $|k|$ раз (радиус-вектор становится длиннее в $|k|$ раз).

Примечание 4

Графическая интерпретация операции умножения заданного комплексного числа $z=a+b\cdot i$ на число $k\, \, (|k|

«Умножение комплексных чисел» 👇

Помощь эксперта по теме работы

Найти эксперта

Решение задач от ИИ за 2 минуты

Решить задачу

Помощь с рефератом от нейросети

Написать ИИ

Иллюстрация примера умножения заданного комплексного числа $z=a+b\cdot i$ на число $k_{1} =2,\, \, k_{2} =\frac{1}{4} $ с использованием комплексной плоскости приведена на рис.1-2.

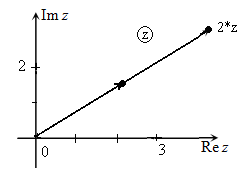
Иллюстрация примера умножения заданного комплексного числа

Рис. 1

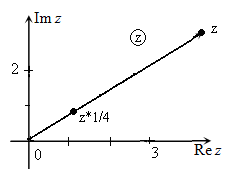
Иллюстрация примера умножения заданного комплексного числа

Рис. 2

Определение 2

Произведением двух заданных комплексных чисел $z_{1} =a_{1} +b_{1} i$ и $z_{2} =a_{2} +b_{2} i$ является комплексное число, которое получается перемножением данных чисел по правилам алгебры с учетом того, что $i^{2} =-1$.

Пример 2

Вычислить $i^{k} $ для $k=3..7$.

Решение:

\[i^{2} =-1\]

\[i^{3} =i^{2} \cdot i=-1\cdot i=-i\]

\[i^{4} =i^{2} \cdot i^{2} =-1\cdot (-1)=1\]

\[i^{5} =i^{2} \cdot i^{3} =-1\cdot (-i)=i\]

\[i^{6} =(i^{2} )^{3} =(-1)^{3} =-1\]

\[i^{7} =(i^{2} )^{3} \cdot i=(-1)^{3} \cdot i=-1\cdot i=-i\]

Пример 3

Выполнить умножение комплексных чисел:

1) $z_{1} =1+3i$ и $z_{2} =3-5i$; 2) $z_{1} =\sqrt{3} +2i$ и $z_{2} =\sqrt{5} \cdot i$.

Решение:

Для умножения комплексных чисел воспользуемся определением и получим:

1) $z_{1} \cdot z_{2} =(1+3i)\cdot (3-5i)=1\cdot 3+3\cdot 3i+1\cdot (-5i)+3i\cdot (-5i)=3+9i-5i-15i^{2} =3+4i+15=18+4i$

2)\[\begin{array}{l} {z_{1} \cdot z_{2} =(\sqrt{3} +2i)\cdot (0+\sqrt{5} \cdot i)=\sqrt{3} \cdot 0+0\cdot 2i+\sqrt{3} \cdot \sqrt{5} \cdot i+2i\cdot \sqrt{5} \cdot i=0+0+\sqrt{15} \cdot i+2\sqrt{5} \cdot i^{2} =\sqrt{15} \cdot i-2\sqrt{5} =-2\sqrt{5} +\sqrt{15} \cdot i} \end{array}\]

Замечание 1

Произведение комплексно-сопряженных чисел $z=a+b\cdot i$ и $\overline{z}=a-b\cdot i$ определяется равенством

\[z\cdot \overline{z}=a^{2} +b^{2} \]

или

\[z\cdot \overline{z}=|z|^{2} =|\overline{z}|^{2} .\]

Другими словами, произведение комплексно-сопряженных чисел есть квадрат модуля каждого из них.

Пример 4

Выполнить умножение комплексно-сопряженных чисел, используя замечание 1 и определение:

1) $z=1+3i$ и $\overline{z}=1-3i$; 2) $z=\sqrt{3} +2i$ и $\overline{z}=\sqrt{3} -2i$.

Решение:

Для умножения комплексных чисел воспользуемся замечанием 1 и получим:

1) $z\cdot \overline{z}=(1+3i)\cdot (1-3i)=1^{2} +3^{2} =1+9=10$

2) \[z\cdot \overline{z}=(\sqrt{3} +2i)\cdot (\sqrt{3} -2i)=(\sqrt{3} )^{2} +2^{2} =3+4=7\]

Для умножения комплексных чисел воспользуемся определением и получим:

1) $z\cdot \overline{z}=(1+3i)\cdot (1-3i)=1\cdot 1+1\cdot 3i+1\cdot (-3i)+3i\cdot (-3i)=1+3i-3i-9i^{2} =1+9=10$

2) $\begin{array}{l} {z\cdot \overline{z}=(\sqrt{3} +2i)\cdot (\sqrt{3} -2i)=\sqrt{3} \cdot \sqrt{3} +\sqrt{3} \cdot 2i-\sqrt{3} \cdot 2\cdot i+2i\cdot (-2)\cdot i=3+2\sqrt{3} \cdot i-2\sqrt{3} \cdot i-2^{2} \cdot i^{2} =3+4=7} \end{array}$

Результаты выполнения операции умножения комплексных чисел совпадают.

Определение 3

Произведением двух заданных комплексных чисел в тригонометрической форме $z_{1} =r_{1} \cdot (\cos \varphi _{1} +i\sin \varphi _{1} )$ и $z_{2} =r_{2} \cdot (\cos \varphi _{2} +i\sin \varphi _{2} )$ является комплексное число, которое определяется равенством

\[z_{1} \cdot z_{2} =r_{1} \cdot r_{2} \cdot [\cos (\varphi _{1} +\varphi _{2} )+i\sin (\varphi _{1} +\varphi _{2} )].\]

Пример 5

Выполнить умножение комплексных чисел:

1) $z_{1} =\sqrt{3} \cdot (\cos \frac{\pi }{4} +i\cdot \sin \frac{\pi }{4} )$ и $z_{2} =2\cdot (\cos \frac{2\pi }{3} +i\cdot \sin \frac{2\pi }{3} )$;

2) $z_{1} =4\cdot (\cos \pi +i\cdot \sin \pi )$ и $z_{2} =5\cdot (\cos \frac{\pi }{2} +i\cdot \sin \frac{\pi }{2} )$.

Решение:

Для умножения комплексных чисел воспользуемся определением и получим:

1) $\begin{array}{l} {z_{1} \cdot z_{2} =\left(\sqrt{3} \cdot (\cos \frac{\pi }{4} +i\cdot \sin \frac{\pi }{4} )\right)\cdot \left(2\cdot (\cos \frac{2\pi }{3} +i\cdot \sin \frac{2\pi }{3} )\right)=2\cdot \sqrt{3} \cdot [\cos (\frac{\pi }{4} +\frac{2\pi }{3} )+i\cdot \sin (\frac{\pi }{4} +\frac{2\pi }{3} )]=2\sqrt{3} \cdot (\cos \frac{11\pi }{12} +i\cdot \sin \frac{11\pi }{12} )} \end{array}$

2) \[\begin{array}{l} {z_{1} \cdot z_{2} =\left(4\cdot (\cos \pi +i\cdot \sin \pi )\right)\cdot \left(5\cdot (\cos \frac{\pi }{2} +i\cdot \sin \frac{\pi }{2} )\right)=4\cdot 5\cdot [\cos (\pi +\frac{\pi }{2} )+i\cdot \sin (\pi +\frac{\pi }{2} )]=20\cdot (\cos \frac{3\pi }{2} +i\cdot \sin \frac{3\pi }{2} )} \end{array}\]

Определение 4

Произведением двух заданных комплексных чисел в показательной форме $z_{1} =r_{1} \cdot e^{i\varphi _{1} } $ и $z_{2} =r_{2} \cdot e^{i\varphi _{2} } $ является комплексное число, которое определяется равенством

\[z_{1} \cdot z_{2} =r_{1} \cdot e^{i\varphi _{1} } \cdot r_{2} \cdot e^{i\varphi _{2} } =r_{1} \cdot r_{2} \cdot e^{i(\varphi _{1} +\varphi _{2} )} .\]

Пример 6

Выполнить умножение комплексных чисел:

1) $z_{1} =\sqrt{3} \cdot e^{i\cdot \frac{\pi }{4} } $ и $z_{2} =2\cdot e^{i\cdot \frac{\pi }{3} } $; 2) $z_{1} =\sqrt{5} \cdot e^{i\cdot \frac{2\pi }{3} } $ и $z_{2} =2\cdot e^{i\cdot \frac{\pi }{2} } $.

Решение:

Для умножения комплексных чисел воспользуемся определением и получим:

1) \[z_{1} \cdot z_{2} =\left(\sqrt{3} \cdot e^{i\cdot \frac{\pi }{4} } \right)\cdot \left(2\cdot e^{i\cdot \frac{\pi }{3} } \right)=2\cdot \sqrt{3} \cdot e^{i\cdot (\frac{\pi }{4} +\frac{\pi }{3} )} =2\sqrt{3} \cdot e^{i\cdot \frac{7\pi }{12} } \]

2) \[z_{1} \cdot z_{2} =\left(\sqrt{5} \cdot e^{i\cdot \frac{2\pi }{3} } \right)\cdot \left(2\cdot e^{i\cdot \frac{\pi }{2} } \right)=2\cdot \sqrt{5} \cdot e^{i\cdot (\frac{2\pi }{3} +\frac{\pi }{2} )} =2\sqrt{3} \cdot e^{i\cdot \frac{7\pi }{6} } \]

Дата последнего обновления статьи: 13.11.2024