Экстремумы функции
Для того чтобы ввести понятие наибольшего и наименьшего значения функций, вначале познакомимся с таким понятием, как экстремумы функций. Это понятие нам будет необходимо не для самого определения значений таких функций, а для построения схемы нахождения таких промежутков для конкретно заданных функций.
Точка $x'$ входящая в область определения функции называется точкой экстремума, если она либо будет точкой максимума, либо будет точкой минимума для функции $f(x)$.
Точка $x'$ будет называться точкой максимума для введенной функции $f(x)$, если у она имеет такую окрестность, что для всех точек $x$, которые входят в эту окрестность, будет верно $f(x)\le f(x'{\rm \ })$.
Точка $x_0$ будет называться точкой минимума для введенной функции $f(x)$, если она имеет такую окрестность, что для всех точек $x$, которые входят в эту окрестность, будет верно $f(x)\ge f(x'{\rm \ })$.
Чтобы полностью разобраться в данном понятии, далее введем понятие критической точки функции.
Точка $x'$ будет называться критической точкой для данной функции $f(x)$, если выполняются два следующих условия:
- Точка $x'$ является внутренней точкой для области определения данной функции;
- $f'\left(x'{\rm \ }\right)=0$ или не существует.
Сформулируем без доказательства теоремы о необходимом (теорема 1) и достаточном (теорема 2) условии для существования точки экстремума.
Если $y=f(x)$ имеет экстремум в точке $x_0$, то либо её производная в ней равняется нулю, либо производная в ней не существует.
Пусть точка $x'$ будет критической для $y=f(x)$ и принадлежит интервалу $(a,b)$, причем на каждом интервале $\left(a,x'{\rm \ }\right)\ и\ (x'{\rm \ },b)$ производная $f'(x)$ существует и сохраняет один и тот же знак. В этом случае:
- Если в $(a,x'{\rm \ })$ $f'\left(x\right) >0$, а в $(x'{\rm \ },b)$ $f'\left(x\right)
- Если в $(a,x'{\rm \ })$ $f'\left(x\right)0$, то $x'$ --будет точкой минимума для этой функции.
- Если и в $(a,x'{\rm \ })$, и в $(x'{\rm \ },b)$ производная $имеет\ один\ и\ тот\ же\ постоянный\ знак$, то $x'$ не будет точкой экстремума для этой функции.
На рисунке 1 мы можем наглядно увидеть смысл теоремы 2.
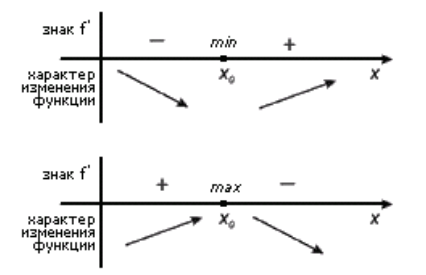
Рисунок 1.
Примеры точек экстремумов вы можете видеть на рисунке 2.
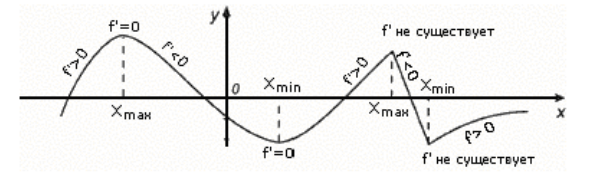
Рисунок 2.
Правило исследования на экстремум
- Найти $D(f)$;
- Найти $f'(x)$;
- Найти точки, где $f'\left(x\right)=0$;
- Найти точки, где $f'(x)$ не будет существовать;
- Отметить на координатной прямой $D(f)$ и все найденные в 3 и 4 пункте точки;
- Определить знак $f'(x)$ на полученных промежутках;
- Используя теорему 2, сделать заключение по поводу всех найденных точек.
Понятие наибольшего и наименьшего значений
Функция $y=f(x)$, которая имеет областью определения множество $X$, имеет наибольшее значение в точке $x'\in X$, если выполняется
\[f\left(x\right)\le f(x')\]Функция $y=f(x)$, которая имеет областью определения множество $X$, имеет наименьшее значение в точке $x'\in X$, если выполняется
\[f\left(x\right)\ge f(x')\]Чтобы найти наименьшее и наибольшее значение заданной функции на каком либо отрезке необходимо произвести следующие действия:
- Найти $f'(x)$;
- Найти точки, в которых $f'\left(x\right)=0$;
- Найти точки, в которых $f'(x)$ не будет существовать;
- Выкинуть из точек, найденных в пунктах 2 и 3 те, которые не лежат в отрезке $[a,b]$;
- Вычислить значения в оставшихся точках и на концах $[a,b]$;
- Выбрать из этих значений наибольшее и наименьшее.
Примеры задач
Найти наибольшее и наименьшее значения на [0,6]: $f\left(x\right)=x^3-3x^2-45x+225$
Решение.
- $f'\left(x\right)=3x^2-6x-45$;
- $f'\left(x\right)=0$;
- \[3x^2-6x-45=0\]
- \[x^2-2x-15=0\]
- \[x=5,\ x=-3\]
- $f'(x)$ существует на всей $D(f)$;
- $5\in \left[0,6\right]$;
-
Значения:
\[f\left(0\right)=225\] \[f\left(5\right)=50\] \[f\left(6\right)=63\] -
Наибольшее значение равняется $225$, наименьшее равняется $50.$
Ответ: $max=225,\ min=50$.
Найти наибольшее и наименьшее значения на [-1,1]:$f\left(x\right)=\frac{x^2-4x+4}{x-2}$
Решение.
\[f\left(x\right)=\frac{x^2-4x+4}{x-2}=\frac{{(x-2)}^2}{x-2}=x-2,\ x\ne 2\]-
$f'\left(x\right)=(x-2)'=1$;
Точек экстремума нет.
-
Значения:
\[f\left(-1\right)=-3\] \[f\left(1\right)=-1\]
Ответ: $max=-1,\ min=-3$.











