Понятие площади
Понятие площади многоугольника будем связывать с такой геометрической фигурой, как квадрат. За единицу площади многоугольника будем принимать площадь квадрата со стороной, равной единице. Введем два основных свойства, для понятия площади многоугольника.
Далее введем площади основных фигур планиметрии: квадрата, прямоугольника, параллелограмма, трапеции и треугольника без их вывода.
Площадь квадрата
Площадь квадрата определяется как квадрат длины его стороны, то есть
\[S=a^2\]Площадь прямоугольника
Площадь прямоугольника определяется произведением длин его смежных сторон, то есть
\[S=ab\]Площадь параллелограмма
Площадь параллелограмма определяется как произведение длины его стороны, на высоту, проведенную к ней, то есть
\[S=ah\]Площадь параллелограмма определяется как произведение длины его смежных сторон, на синус угла между этими сторонами, то есть
\[S=absin\alpha \]Площадь трапеции
Площадь трапеции определяется как половина произведения суммы длин его оснований, на его высоту, то есть
\[S=\frac{1}{2}(a+b)h\]Площадь треугольника
Площадь треугольника определяется как половина произведения длины его стороны, на высоту, проведенную к ней, то есть
\[S=\frac{1}{2}ah\][Теорема] Площадь треугольника определяется как половина произведения длины его смежных сторон, на синус угла между этими сторонами, то есть
[/Теорема]
Пусть нам даны три стороны треугольника $a,\ b\ и\ c$. Тогда площадь этого треугольника выражается следующим образом
\[S=\sqrt{p\left(p-a\right)\left(p-b\right)(p-c)}\]где $p$ - полупериметр данного треугольника.
Площадь правильного треугольника со стороной $a$ определяется следующим образом
\[S=\frac{a^2\sqrt{3}}{4}\]Пусть нам даны три стороны треугольника $a,\ b\ и\ c$ и радиус вписанной в него окружности $r$. Тогда площадь этого треугольника выражается следующим образом
\[S=pr\]где $p$ - полупериметр данного треугольника.
Пусть нам даны три стороны треугольника $a,\ b\ и\ c$ и радиус описанной около него окружности $R$. Тогда площадь этого треугольника выражается следующим образом
\[S=\frac{abc}{4R}\]Пример задач
Найти площадь фигуры, данной на рисунке $1$, если одна клетка имеет площадь, равную единице.
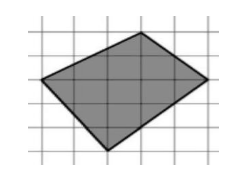
Рисунок 1.
Решение.
Данную фигуру можно разбить следующим образом:
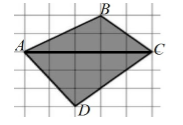
Рисунок 2.
По теореме $6$, имеем
\[S_{ADC}=\frac{1}{2}\cdot 5\cdot 3=7,5,\ \ S_{ABC}=\frac{1}{2}\cdot 5\cdot 2=5\ \]$\ $Тогда
\[S=S_{ADC}+S_{ABC}=7,5+5=12,5\]Найти площадь фигуры, данной на рисунке $2$, если одна клетка имеет площадь, равную единице.
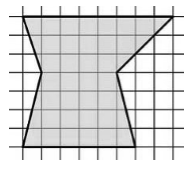
Рисунок 3.
Решение.
Данную фигуру можно разбить следующим образом:
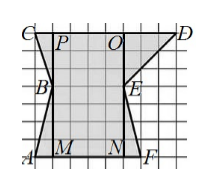
Рисунок 4.
По теореме $6$, имеем
\[S_{ABM}=\frac{1}{2}\cdot 4\cdot 1=2,\ \ S_{BCP}=\frac{1}{2}\cdot 3\cdot 1=1,5,\ \ S_{OED}=\frac{1}{2}\cdot 3\cdot 3=4,5,\ \ S_{ENF}=\frac{1}{2}\cdot 4\cdot 1=2\]По теореме $2$, имеем
\[S_{MNOP}=4\cdot 7=28\]Тогда
\[S=S_{ABM}+S_{BCP}+S_{OED}+S_{ENF}+S_{MNOP}=\] \[=2+1,5+4,5+2+28=38\]Ответ: $38$.











