Тригонометрические уравнения
Тригонометрические уравнения вида $\cos x=C$, $\sin x=C$, $tgx=C$, $ctgx=C$ относятся к простейшим.
Методы решения простейших тригонометрических уравнений известны и они являются основой для решения более сложных тригонометрических уравнений. Существует ряд подходов для решения более сложных тригонометрических уравнений:
а) с помощью алгебраических преобразований или тригонометрических формул некоторые уравнения могут быть сведены к простейшим тригонометрическим уравнениям;
б) если тригонометрическое уравнение содержит только одну какую-либо тригонометрическую функцию с одним и тем же аргументом, то вводят для неё некоторое обозначение в виде новой переменной и получают алгебраическое уравнение относительно этой переменной;
в) используя тригонометрические формулы, часто удается привести тригонометрическое уравнение к одной какой-либо тригонометрической функции с одним и тем же аргументом, после чего остается применить замену переменных;
г) иногда уравнение удается разложить на несколько сомножителей;
д) тригонометрические уравнения вида $a\cdot \sin x+b\cdot \cos x=0$, где $a\ne 0$, $b\ne 0$, называются однородными; для них также существуют специфические методы решения.
Уравнения $\cos x=C$, $\sin x=C$, $tgx=C$
Таблица вариантов решений уравнения $\sin x=C$:

Рисунок 1.
Решить уравнение $\sin \left(x+\frac{\pi }{8} \right)=-\frac{\sqrt{2} }{2} $.
\[\left|-\frac{\sqrt{2} }{2} \right|Таблица вариантов решений уравнения $\cos x=C$: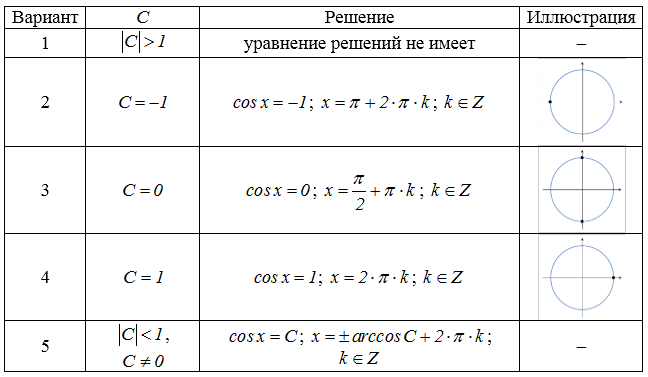
Рисунок 2.
Решить уравнение $\cos \left(3\cdot x\right)=0$.
\[3\cdot x=\frac{\pi }{2} +\pi \cdot k; x=\frac{\pi }{6} +\frac{\pi }{3} \cdot k; k\in Z. \]Решение уравнений $tgx=C$, $ctgx=C$.
Множество решений уравнения $tgx=C$ имеет следующий вид: $x=arctgC+\pi \cdot k$, $k\in Z$.
Решить уравнение $tg\left(2\cdot x\right)=\sqrt{3} $.
\[2\cdot x=arctg\sqrt{3} +\pi \cdot k; 2\cdot x=\frac{\pi }{3} +\pi \cdot k; x=\frac{\pi }{6} +\frac{\pi }{2} \cdot k; k\in Z.\]Множество решений уравнения $ctgx=C$ имеет следующий вид: $x=arcctgC+\pi \cdot k$, $k\in Z$.
Решить уравнение $ctg\left(x+\frac{\pi }{3} \right)=-\frac{1}{\sqrt{3} } \sqrt{3} $.
\[x+\frac{\pi }{3} =arcAtg\left(-\frac{1}{\sqrt{3} } \right)+\pi \cdot k; x=-\frac{\pi }{3} +\frac{2\cdot \pi }{3} +\pi \cdot k; x=\frac{\pi }{3} +\pi \cdot k; k\in Z.\]Решить уравнение $4\cdot \sqrt{3} \cdot tg\left(-\frac{x}{3} \right)-4=0$.
С помощью алгебраических преобразований получим простейшее тригонометрическое уравнение.
Поскольку $tg\left(-\frac{x}{3} \right)=-tg\frac{x}{3} $, то имеем:
\[-4\cdot \sqrt{3} \cdot tg\frac{x}{3} -4=0; \sqrt{3} \cdot tg\frac{x}{3} +1=0; tg\frac{x}{3} =-\frac{1}{\sqrt{3} } ;\] \[\frac{x}{3} =arctg\left(-\frac{1}{\sqrt{3} } \right)+\pi \cdot k; \frac{x}{3} =-\frac{\pi }{6} +\pi \cdot k; x=-\frac{\pi }{2} +3\cdot \pi \cdot k; k\in Z. \]Решить уравнение $\cos ^{2} \left(4\cdot x\right)-\sin ^{2} \left(4\cdot x\right)=\frac{\sqrt{3} }{2} $.
С помощью алгебраических преобразований и тригонометрических формул получим простейшее тригонометрическое уравнение.
В левой части уравнения используем формулу двойного угла и получаем: $\cos \left(8\cdot x\right)=\frac{\sqrt{3} }{2} $. Отсюда следует: $8\cdot x=\pm \arccos \frac{\sqrt{3} }{2} +2\cdot \pi \cdot k$; $8\cdot x=\pm \frac{\pi }{6} +2\cdot \pi \cdot k$; $x=\pm \frac{\pi }{48} +\frac{1}{4} \cdot \pi \cdot k$; $k\in Z$.
Решить уравнение $\sin \left(4\cdot x\right)\cdot \cos x-\cos \left(4\cdot x\right)\cdot \sin x=-1$.
С помощью алгебраических преобразований получим простейшее тригонометрическое уравнение.
Преобразуем левую часть уравнения: $\sin \left(4\cdot x-x\right)=-1$. Отсюда получаем: $\sin \left(3\cdot x\right)=-1$; $3\cdot x=-\frac{\pi }{2} +2\cdot \pi \cdot k$; $x=-\frac{\pi }{6} +\frac{2}{3} \cdot \pi \cdot k$; $k\in Z$.
Решить уравнение $\sin ^{2} x-4\cdot \sin x+3=0$.
В данной задаче используем замену.
Обозначаем $\sin x=z$, $\left|z\right|\le 1$. Получаем квадратное уравнение $z^{2} -4\cdot z+3=0$, корни которого $z_{1} =1$, $z_{2} =3$. Поскольку $\left|z\right|\le 1$, то подходит только корень $z_{1} =1$.
Получаем: $\sin x=1$; $x=\frac{\pi }{2} +2\cdot \pi \cdot k$; $k\in Z$.












