Перед изучением функции тангенса и её свойств, вспомним понятие самого тангенса. Определение тангенса можно ввести двумя способами: с помощью прямоугольного треугольника и с помощью понятий синуса и косинуса.
Тангенсом острого угла называется отношение длины противолежащего катета к прилежащему катету прямоугольного треугольника (рис 1):
\[cos\alpha =\frac{a}{b}\]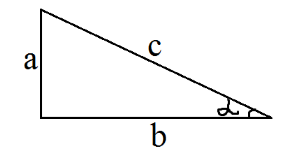
Рисунок 1. Прямоугольный треугольник.
Тангенсом угла называется отношение значения синуса этого угла к значению косинуса этого угла.
Введем таблицу некоторых значений тангенса (таблица 1).
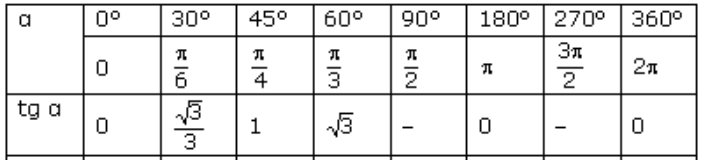
Рисунок 2. Значения тангенса.
Геометрический смысл
Рассмотрим тригонометрическую единичную окружность и прямую $x=1$. Ордината точки $B$ на прямой $x=1$ является тангенсом угла $\alpha $ (рис. 2).
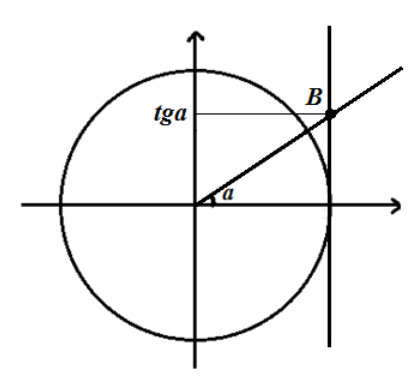
Рисунок 3. Значение тангенса с помощью единичной окружности.
Поэтому, когда точка $B$ опишет вертикальную прямую $x=1$ её ордината примет все значения множества действительных чисел, откуда $tg\alpha $ -- вся числовая прямая. Поэтому прямая $x=1$ называется линией тангенсов.
Свойства функции $f(x)=tgx$
Рассмотрим теперь свойства функции $f\left(x\right)=tgx$.
- По определению 2, получим, что область определения$x\in {\mathbb R}{\rm ,}{\rm \ }x\ne \frac{\pi }{2}+\pi n,\ n\in Z$.
- Из геометрического смысла следует, что область значения -- все числа.
- $f\left(-x\right)={tg \left(-x\right)\ }=-tgx=-f(x)$, следовательно, функция$f\left(x\right)=tgx$ нечетна.
- $f\left(x+\pi \right)={tg \left(x+\pi \right)\ }=tgx=f(x)$, следовательно, функция$f\left(x\right)=tgx$ периодическая с минимальным периодом $\pi $.
- Пересечение с осями координат:
При $x=0$, $f\left(0\right)=tg0=0$.
При $y=0$, $x=\pi n,n\in Z$.
- Функция выше оси $Ox$ при $x\in (\pi n,\frac{\pi }{2}+\pi n),n\in Z$.
- Функция ниже оси $Ox$ при $x\in (-\frac{\pi }{2}+\pi n,\frac{\pi }{2}+\pi n),n\in Z$.
- $f'\left(x\right)={\left(tgx\right)}'=\frac{1}{{cos}^2x}$.
Функция $f\left(x\right)=tgx$ возрастает, при $x\in \left(-\frac{\pi }{2}+\pi n,\frac{\pi }{2}+\pi n\right)$.
-
Функция имеет точку разрыва второго рода при $x=\frac{\pi }{2}+\pi n,\ n\in Z$.
-
${\mathop{lim}_{x\to \frac{\pi }{2}+\pi n-0} tgx\ }=-\infty $, ${\mathop{lim}_{x\to \frac{\pi }{2}+\pi n+0} tgx\ }=+\infty $,
График функции $y=tgx$
Графиком функции $y=tgx$ является тангенсоида (рис. 3).
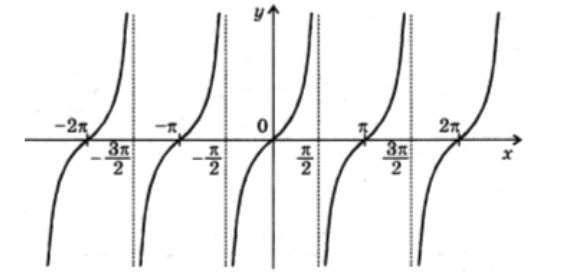
Рисунок 4. Тангенсоида.
Задача на построение тангенсоиды
Построить график функции $y=tg(x-2\pi )$.
Так как $tgx$ периодическая с минимальным периодом $\pi $, то получим, что $y=tg\left(x-2\pi \right)=tg\left(x-\pi \right)=tgx$. Получаем график:
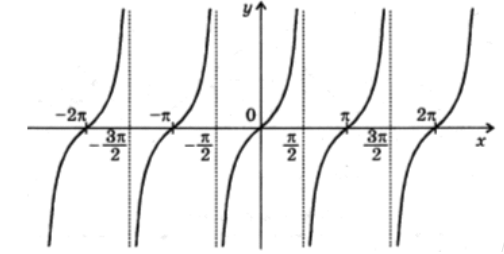
Рисунок 5.












