Зависимость между синусом, косинусом и тангенсом одного и того же угла
Тригонометрические функции в случае произвольного угла $-\infty
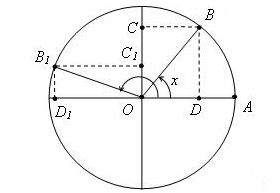
Рисунок 1.
В этом круге проведены горизонтальный и вертикальный диаметры, которые разделяют круг на квадранты. Неподвижный радиус $OA$ совпадает с горизонтальным диаметром и считается началом отсчета углов $x$, которые образует с ним подвижный радиус $OB$. При этом углы полагают положительными, если их отсчитывают против часовой стрелки, и отрицательными, если их отсчитывают в противоположном направлении. Проекциям подвижного радиуса $OB$ на диаметры приписывается знак, а именно: проекции, расположенные выше и справа центра $O$ - положительные, слева и ниже центра $O$ - отрицательные.
Заметим также, что в единичном круге угол $x$ равняется удвоенной площади $S$ сектора $OAB$. Действительно, $S=\frac{x\cdot R^{2} }{2} $, откуда $x=2\cdot S$ при $R=1$.
По определению, тригонометрические функции связанны с проекциями подвижного радиуса на диаметры тригонометрического круга и вводятся следующим образом: $\sin x=OC$, $\cos x=OD$, $tgx=\frac{\sin x}{\cos x} $, $ctgx=\frac{\cos x}{\sin x} $.
Непосредственно из рисунка можно установить следующие основные свойства тригонометрических функций, из которых вытекают все другие:
-
основное тригонометрическое тождество $\sin ^{2} x+\cos ^{2} x=1$;
-
функции $\sin x$ и $\cos x$ периодические с основным периодом $2\cdot \pi $, функции $tgx$ и $ctgx$ периодические с основным периодом $\pi $;
-
функции $\sin x$ и $\cos x$ являются ограниченными, то есть $\left|\sin x\right|\le 1$, $\left|\cos x\right|\le 1$;
-
функция $\cos x$ четная, то есть $\cos \left(-x\right)=\cos x$; остальные функции -- нечетные, например, $\sin \left(-x\right)=-\sin x$;
-
полуоборот в любую сторону меняет знак синуса и косинуса, то есть $\sin \left(x\pm \pi \right)=-\sin x$, $\cos \left(x\pm \pi \right)=-\cos x$, и не меняет знак тангенса и котангенса, то есть $tg\left(x\pm \pi \right)=tgx$, $ctg\left(x\pm \pi \right)=ctgx$;
-
угол, который дополняет данный к $\frac{\pi }{2} $, меняет наименование функции, то есть $\sin \left(\frac{\pi }{2} -x\right)=\cos x$, $\cos \left(\frac{\pi }{2} -x\right)=\sin x$, $tg\left(\frac{\pi }{2} -x\right)=ctgx$, $ctg\left(\frac{\pi }{2} -x\right)=tgx$;
-
функция $tgx$ не существует, если $\cos x=0$, то есть $x=\frac{\pi }{2} \cdot \left(2\cdot n+1\right),\; n\in Z$; функция $ctgx$ не существует, если $\sin x=0$, то есть $x=\pi \cdot n,\; n\in Z$.
Тригонометрические тождества
Тождественность двух тригонометрических выражений предполагает, что из рассмотрения исключаются те значения входящих в них букв, при которых хотя бы одно из выражений теряет смысл.
Доказать тождество $\sin \left(4\cdot \alpha \right)+\cos \left(4\cdot \alpha \right)\cdot ctg\left(2\cdot \alpha \right)=\frac{1-tg^{2} \alpha }{2\cdot tg\alpha } $.
\[\sin \left(4\cdot \alpha \right)+\cos \left(4\cdot \alpha \right)\cdot ctg\left(2\cdot \alpha \right)=\sin \left(4\cdot \alpha \right)+\cos \left(4\cdot \alpha \right)\cdot \frac{\cos \left(2\cdot \alpha \right)}{\sin \left(2\cdot \alpha \right)} =\] \[=\frac{\sin \left(4\cdot \alpha \right)\cdot \sin \left(2\cdot \alpha \right)+\cos \left(4\cdot \alpha \right)\cdot \cos \left(2\cdot \alpha \right)}{\sin \left(2\cdot \alpha \right)} =\frac{\cos \left(4\cdot \alpha -2\cdot \alpha \right)}{\sin \left(2\cdot \alpha \right)} =\] \[=\frac{\cos \left(2\cdot \alpha \right)}{\sin \left(2\cdot \alpha \right)} =ctg\left(2\cdot \alpha \right)=\frac{1}{tg\left(2\cdot \alpha \right)} =\frac{1-tg^{2} \alpha }{2\cdot tg\alpha } .\]Доказать тождество $\sin x\cdot \left(1+tgx\cdot tg\frac{x}{2} \right)=tgx$.
\[\sin x\cdot \left(1+tgx\cdot tg\frac{x}{2} \right)=\sin x\cdot \frac{\cos x\cdot \cos \frac{x}{2} +\sin x\cdot \sin \frac{x}{2} }{\cos x\cdot \cos \frac{x}{2} } =\] \[=\sin x\cdot \frac{\cos \left(x-\frac{x}{2} \right)}{\cos x\cdot \cos \frac{x}{2} } =\sin x\cdot \frac{\cos \frac{x}{2} }{\cos x\cdot \cos \frac{x}{2} } =\frac{\sin x}{\cos x} =tgx.\]Доказать тождество
\[tg\left(3\cdot \alpha \right)-tg\left(2\cdot \alpha \right)-tg\alpha =tg\alpha \cdot tg\left(2\cdot \alpha \right)\cdot tg\left(3\cdot \alpha \right).\] \[tg\left(3\cdot \alpha \right)-tg\left(2\cdot \alpha \right)-tg\alpha =\] \[=tg\left(3\cdot \alpha \right)-\frac{tg\left(2\cdot \alpha \right)+tg\alpha }{1-tg\left(2\cdot \alpha \right)\cdot tg\alpha } \cdot \left(1-tg\left(2\cdot \alpha \right)\cdot tg\alpha \right)=\] \[=tg\left(3\cdot \alpha \right)-tg\left(3\cdot \alpha \right)\cdot \left(1-tg\left(2\cdot \alpha \right)\cdot tg\alpha \right)=tg\alpha \cdot tg\left(2\cdot \alpha \right)\cdot tg\left(3\cdot \alpha \right).\]Доказать тождество
\[ctg\alpha -tg\alpha -2\cdot tg\left(2\cdot \alpha \right)-4\cdot tg\left(4\cdot \alpha \right)=8\cdot ctg\left(8\cdot \alpha \right).\] \[ctg\alpha -tg\alpha -2\cdot tg\left(2\cdot \alpha \right)-4\cdot tg\left(4\cdot \alpha \right)=\] \[=\frac{\cos ^{2} \alpha -\sin ^{2} \alpha }{\cos \alpha \cdot \sin \alpha } -2\cdot tg\left(2\cdot \alpha \right)-4\cdot tg\left(4\cdot \alpha \right)=\] \[=\frac{2\cdot \cos \left(2\cdot \alpha \right)}{\sin \left(2\cdot \alpha \right)} -\frac{2\cdot \sin \left(2\cdot \alpha \right)}{\cos \left(2\cdot \alpha \right)} -4\cdot tg\left(4\cdot \alpha \right)=\] \[=\frac{2\cdot \left(\cos ^{2} \left(2\cdot \alpha \right)-\sin ^{2} \left(2\cdot \alpha \right)\right)}{\sin \left(2\cdot \alpha \right)\cdot \cos \left(2\cdot \alpha \right)} -4\cdot tg\left(4\cdot \alpha \right)=\] \[=\frac{4\cdot \cos \left(4\cdot \alpha \right)}{\sin \left(4\cdot \alpha \right)} -\frac{4\cdot \sin \left(4\cdot \alpha \right)}{\cos \left(4\cdot \alpha \right)} =\frac{4\cdot \left(\cos ^{2} \left(4\cdot \alpha \right)-\sin ^{2} \left(4\cdot \alpha \right)\right)}{\sin \left(4\cdot \alpha \right)\cdot \cos \left(4\cdot \alpha \right)} =\] \[=\frac{8\cdot \cos \left(8\cdot \alpha \right)}{\sin \left(8\cdot \alpha \right)} =8\cdot ctg\left(8\cdot \alpha \right).\]Доказать тождество $\frac{\sin y+\sin x\cdot \cos \left(x+y\right)}{\cos y-\sin x\cdot \sin \left(x+y\right)} =tg\left(x+y\right)$.
\[\frac{\sin y+\sin x\cdot \cos \left(x+y\right)}{\cos y-\sin x\cdot \sin \left(x+y\right)} =\frac{\sin y+\frac{1}{2} \cdot \left(\sin \left(2\cdot x+y\right)-\sin y\right)}{\cos y-\frac{1}{2} \cdot \left(\cos y-\cos \left(2\cdot x+y\right)\right)} =\] \[=\frac{\sin y+\sin \left(2\cdot x+y\right)}{\cos y+\cos \left(2\cdot x+y\right)} =\frac{2\cdot \sin \left(x+y\right)\cdot \cos x}{2\cdot \cos \left(x+y\right)\cdot \cos x} =tg\left(x+y\right).\]Вычислить значение выражения $arctg2+arctg3$.
Вычислим тангенс данного выражения. Получим:
\[tg\left(arctg2+arctg3\right)=\frac{tg\left(arctg2\right)+tg\left(arctg3\right)}{1-tg\left(arctg2\right)\cdot tg\left(arctg3\right)} =\frac{2+3}{1-2\cdot 3} =-1.\]Следовательно, $arctg2+arctg3=k\cdot \pi -\frac{\pi }{4} $, где $k$ -- целое число или $0$. Но $\frac{\pi }{4}

















