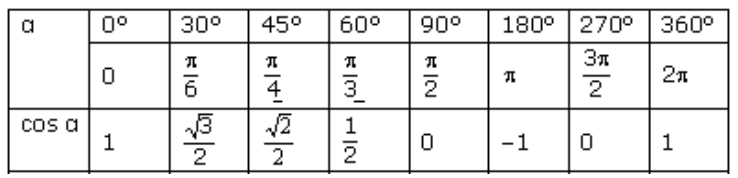
Понятие косинуса
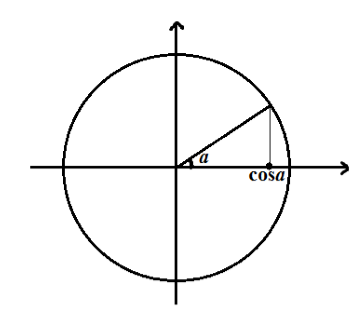
Перед изучением функции косинуса и её свойств, вспомним понятие самого косинуса. Определение косинуса можно ввести двумя способами: с помощью прямоугольного треугольника и с помощью тригонометрической окружности.
Косинусом острого угла называется отношение длины прилежащего катета к гипотенузе прямоугольного треугольника (рис 1):
\[cos\alpha =\frac{b}{c}\]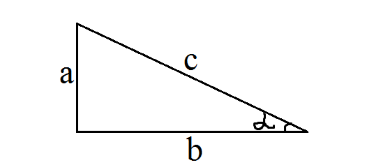
Рисунок 1. Прямоугольный треугольник.
Свойства функции $f(x)=cosx$
Рассмотрим теперь свойства функции $f\left(x\right)=cosx$.
- Область определения -- все числа.
- Так как по определению 2 значение косинуса определяется с помощью единичной окружности, то область значения данной функции отрезок $[-1,\ 1]$.
- $f\left(-x\right)={cos \left(-x\right)\ }=cosx=f(x)$, следовательно, функция $f\left(x\right)=cosx$ четна.
- $f\left(x+2\pi \right)={cos \left(x+2\pi \right)\ }=cosx=f(x)$, следовательно, функция $f\left(x\right)=cosx$ периодическая с минимальным периодом $2\pi $.
-
Пересечение с осями координат: При $x=0$, $f\left(0\right)=cos0=1$. При $y=0$, $x=\frac{\pi }{2}+\pi n,n\in Z$.
-
Функция выше оси $Ox$ при $x\in \left(-\frac{\pi }{2}+2\pi n,\frac{\pi }{2}+2\pi n\right),n\in Z$.
- Функция ниже оси $Ox$ при $x\in \left(\frac{\pi }{2}+2\pi n,\frac{3\pi }{2}+2\pi n\right),n\in Z$.
- $f' (x)=(cosx)'=-sinx$.\[-sinx=0\] \[sinx=0\] \[x=\pi n,\ n\in Z\]
Функция $f\left(x\right)=cosx$ возрастает, при $x\in (-\pi +2\pi n,2\pi n)$. Функция $f\left(x\right)=cosx$ убывает при $x\in (2\pi n,\pi +2\pi n)$ Точки максимума $(2\pi n,1)$. Точки минимума $(\pi +2\pi n,-1)$.
9.Функция непрерывна на всей области определения.
График функции $y=cosx$
Графиком функции $y=cosx$ является косинусоида (рис. 3).
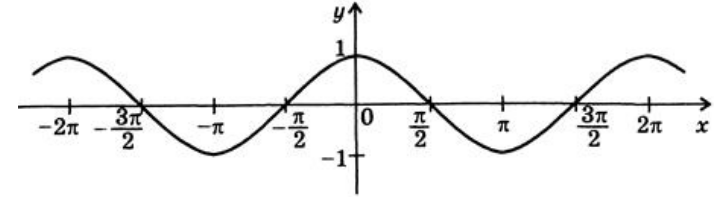
Рисунок 4. Косинусоида.
Задачи на построение косинусоид
Построить график функции $y=2cosx$.
График данной функции получается из функции $y=cosx$ растяжением вдоль оси $Oy$ в 2 раза:
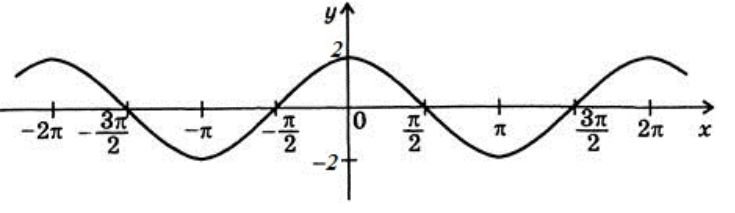
Рисунок 5.
Построить график функции $y=cos\left(x-\frac{\pi }{2}\right)$.
График данной функции получается из функции $y=cosx$ путем смещения вдоль оси $Ox$ на $\frac{\pi }{2}$ единиц вправо.
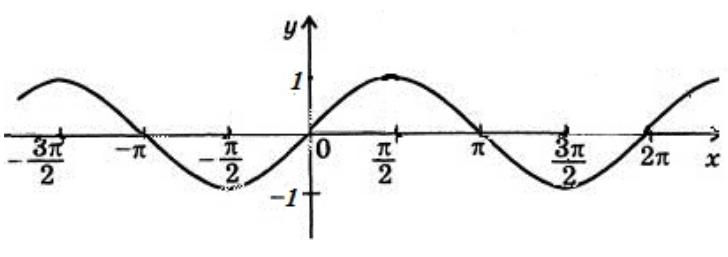
Рисунок 6.