Предмет стереометрии
Стереометрия -- раздел геометрии, изучающий свойства пространственных фигур.
К основным из них относятся -- точка, прямая и плоскость. Точка и прямая известны из планиметрии.
Например, поверхность стола дает представление о части плоскости.
В геометрии считают, что плоскость ровная и неограниченная, не имеет краев и толщины.
На рисунках часть плоскости чаще всего изображают в виде произвольной замкнутой фигуры и обозначают буквами греческого алфавита $\alpha ,\; \beta ,\; \gamma ,\; \ldots $ и т.д.
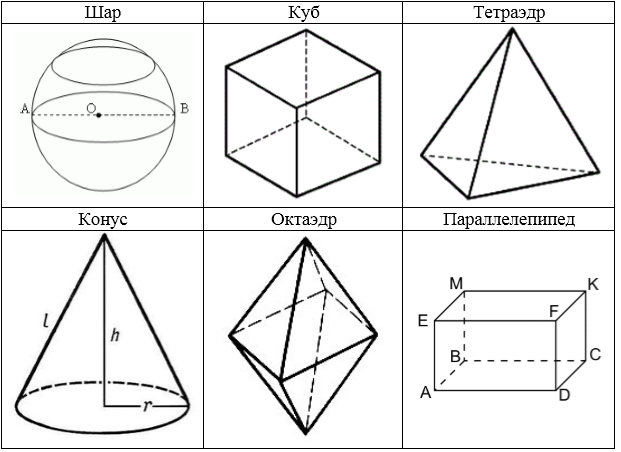
Примеры других популярных фигур стереометрии:
Аксиомы стереометрии
В стереометрии справедливы все аксиомы планиметрии, а именно:
- все точки или принадлежат данной прямой, или не принадлежат ей;
- через любые $2$-е точки можно провести $1$-ну прямую;
- только одна из $3$-х точек на прямой может лежать между $2$-мя другими;
- длина любого отрезка прямой отлична от нуля;
- длина отрезка складывается из длин частей, на которые он делится любой его точкой;
- любой угол имеет определенную меру, отличную от нуля;
- мера угла складывается из мер углов, на которые он делится любым лучем, проходящим между его сторонами;
- аксиома Эвклида -- через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Дополнительные аксиомы стереометрии
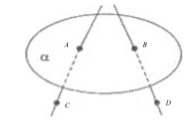
Все точки или принадлежат данной плоскости, или не принадлежат ей. На рисунке точки $A$ и $B$ принадлежат плоскости $\alpha $ (плоскость $\alpha $ проходит через эти точки), а точки $C$ и $D$ -- не принадлежат.
Все точки прямой принадлежат плоскости, если этой плоскости принадлежат любые $2$-е её точки. На рисунке точки $A$ и $B$ прямой $s$ принадлежат плоскости $\alpha $, поэтому и прямая $s$, которой принадлежат эти точки, также принадлежат плоскости $\alpha $.

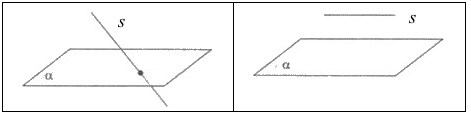
На рисунках ниже представлены два случая, когда прямая $s$ не принадлежит плоскости.
Две плоскости пересекаются по прямой, которая проходит через общую точку этих плоскостей.
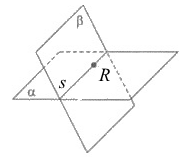
На рисунке плоскости $\alpha $ и $\beta $ имеют общую точку R, то есть точка R принадлежит как плоскости $\alpha $, так и плоскости $\beta $. Точка R принадлежит также прямой $s$. Значит, плоскости $\alpha $ и $\beta $ пересекаются по прямой $s$.
Через любые три точки, не лежащие на одной прямой, можно провести единственную плоскость. Иначе говоря, любые три точки в пространстве всегда лежат в одной плоскости.
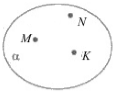
На рисунке точки M, N и K не лежат на $1$-ной прямой. Поэтому существует единственная плоскость $\alpha $, которой принадлежат все эти точки.
Следствия из аксиом стереометрии.
Через прямую $s$ и точку T, не лежащую на ней, можно провести $1$-ну плоскость $\alpha $.

Через $2$-е пересекающиеся прямые p и q можно провести $1$-ну плоскость $\alpha $.
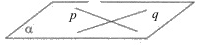
Плоскость можно задать а) $3$-мя точками, не лежащими на $1$-ной прямой, б) прямой и точкой, не лежащей на ней, в) $2$-мя пересекающимися прямыми, г) $2$-мя параллельными прямыми.
Возможны три случая взаимного расположения прямых в пространстве:
- пересекающиеся прямые лежат в $1$-ной плоскости и имеют общую точку;
- параллельные прямые лежат в $1$-ной плоскости и не имеют общих точек;
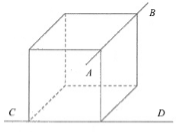
- скрещивающиеся прямые AB и CD -- не лежащие в $1$-ной плоскости.