Вероятность $P\left(X
Обозначение:
\[F\left(x\right)=P\left(XФункция распределения -- универсальная характеристика. Она существует для всех случайных величин -- и непрерывных и дискретных.Свойства функции распределения
- $F\left(x\right)$ - функция неубывающая, т.е. при $x_{1}
По теореме сложения вероятностей несовместных событий получим:
$F\left(x_{2} \right)-F\left(x_{1} \right)=P\left(x_{1} \le X
а поэтому
$F\left(x_{2} \right)-F\left(x_{1} \right)\ge 0$ или $F\left(x_{2} \right)\ge F\left(x_{1} \right)$,
что и требовалось доказать.
- Вероятность того, что случайная величина попадет на участок $\left[a;b\right)$, равна приращению интегральной функции распределения на этом участке.
Это утверждение следует непосредственно из первого свойства. Действительно, если положим $x_{1} =a,{\rm \; }x_{2} =b$, то получим:
Это свойство следует из того, что $\left(X
- $F\left(+\infty \right)=1$.
Это свойство следует из того, что $\left(X
График функции распределения $F\left(x\right)$ есть график неубывающей функции, значения которой меняются от $0$ до $1$.
Применение на практике
В урне находится $7$ шаров, из которых $4$ белых, а остальные черные. Из урны наудачу берут $3$ шара. Найти закон распределения дискретной случайной величины и вероятность события, что вытянут больше чем два белых шара.
Решение.
Пускай $A_{k} $ -- событие, которое состоит в том, что из урны вытянут $k$ белых шаров
Возможные значения случайной величины $k: 0, 1, 2, 3$. Соответствующие им вероятности $р_0$, $р_1$, $р_2$, $р_3$ подсчитываем по формуле:
\[p_{k} =\frac{C_{m}^{k} \cdot C_{n-m}^{s-k} }{C_{n}^{s} } \]Подставляя наши значения, найдем все вероятности.
\[p_{0}=p (x=0)=\frac{C_{4}^{0} \cdot C_{3}^{3} }{C_{7}^{3} }= \frac{1}{35} ; p_{1}=P (x=1)=\frac{C_{4}^{1} \cdot C_{3}^{2} }{C_{7}^{3} }= \frac{12}{35} ;\] \[p_{2}=p (x=2)\, =\frac{C_{4}^{2} \cdot C_{3}^{1} }{C_{7}^{3} }= \frac{18}{35} ; p_{3}=p (x=3)\, =\frac{C_{4}^{3} \cdot C_{3}^{0} }{C_{7}^{3} }=\frac{4}{35} .\]Закон расспределения этой случайной величины будет иметь следующий вид:
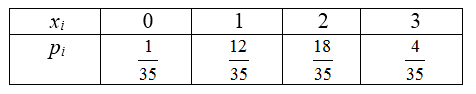
Рисунок 1.
Пускай $А$ -- событие, которое состоит в том, что из урны вытянули больше чем два белых шара. Вероятность этого события будет равна:
\[P(A)=\sum \limits _{k=2}^{3}P(A_{k} ) =\sum \limits _{k=2}^{3}\frac{C_{m}^{k} \cdot C_{n-m}^{s-k} }{C_{n}^{s} } \]Искомая вероятность будет равна:
\[P(A)=P(A_{2} )+P(A_{3} )\]Подставив наши значения получим:
\[P\left(A\right)=\frac{18}{35}+\frac{4}{35}=\frac{22}{35}\]Если в задании заданы натуральные числа $m$, $n$, $s$, причем $m \leq s \leq n$. Если возможными значениями дискретной случайной величины являются $0,1,2,\dots , m$, и вероятности выражаются по формуле:
\[p_k = p(x = k) = $\frac{C_{m}^{k} \cdot C_{n-m}^{s-k} }{C_{n}^{s} } $, k = 0,1,\dots ,m,\]то случайная величина $х$ имеет гипергеометрический закон распределения.
Случайная величина из примера 1 имеет гипергеометрический закон распределения с $n =7$, $s = 3$, $m = 4$.
Среди $50$ изделий $20$ окрашенных. Найти вероятность того, что среди наудачу извлеченных $5$ изделий окажется ровно $3$ окрашенных.
Решение:
По условию задачи $n= 50$, $m = 20$, $s = 5$, $k = 3$. Искомая вероятность
\[P\left(X=3\right)=\frac{C_{20}^{3} C_{30}^{2} }{C_{50}^{5} } =0,234.\]В лотерее «Спортлото» имеется $45$ видов спорта. Студент отметил на карточке шесть видов спорта. Он выиграет, если из этих шести чисел не меньше трьох совпадают с некоторыми шестьма числами, которые выпадают в тираже. Найти вероятность выиграша.
Решение:
Пусть $A_{k} $ - событие, которое состоит в том, что студент угадал $k$ видов спорта. Тогда в формулу:
\[p_{k} =\frac{C_{m}^{k} \cdot C_{n-m}^{s-k} }{C_{n}^{s} } \]подставим наши значения и получим:
\[p_{k} =\frac{C_{6}^{k} \cdot C_{45-6}^{6-k} }{C_{45}^{6} } \]Пусть $А$ -- событие, которое состоит в том, что студент выиграет. Вероятность этого события будет равен:
\[P(A)=\sum \limits _{k=3}^{6}P(A_{k} ) =\sum \limits _{k=3}^{6}\frac{C_{6}^{k} \cdot C_{45-6}^{6-k} }{C_{45}^{6} } \]Закон расспределения этой случайной величины будет иметь следующий вид:

Рисунок 2.
Искомая вероятность будет равна:
\[P(A)=P(A_{3} )+P(A_{4} )+P(A_{5} )+P(A_{6} )\]Подставив полученые значения найдем:
\[P(A)=0,0{\rm 1765}0+0,000{\rm 969}+0,0000{\rm 18}+0,000000\approx 0,018638;\]










