Перед тем, как ввести определения и формулы вычисления основных числовых характеристик системы двух случайных величин напомним, что такое закон распределения.
Законом распределения двумерной случайной величины $(X,Y)$ - называется множество возможных пар чисел $(x_i,\ y_j)$ (где $x_i \epsilon X,\ y_j \epsilon Y$) и их вероятностей $p_{ij}$.
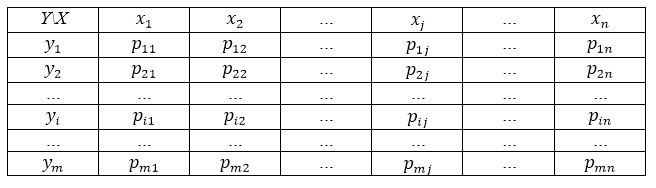
Чаще всего закон распределения двумерной случайной величины записывается в виде таблицы (Таблица 1).
 величины.">
величины.">
Рисунок 1. Закон распределения двумерной случайной величины.
Введем для начала еще два обозначения:
Изобразим теперь дополненную таблицу распределения двумерной случайной величины (таблица 2).
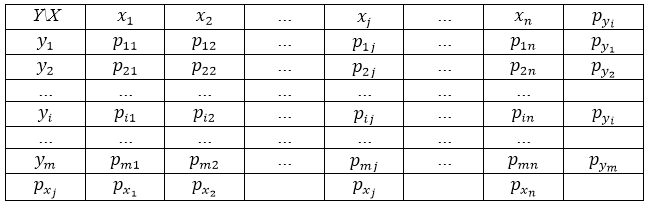
Рисунок 2. Дополненная таблица закона распределения двумерной случайной величины.
Условие нормированности для двумерной случайной величины
Введем для начала условие, которое обязательно должно выполняться для двумерной случайной величины, для которой дана таблица распределения
Основные числовые характеристики для системы двух случайных величин
Рассмотрим теперь основные числовые характеристики для случайных величин $X$ и $Y$, которые включены в систему двух случайных величин $(X,Y)$.
Математическое ожидание:
Среднее квадратического отклонение:
Рассмотрим далее числовые характеристики двумерной случайной величины $(X,Y)$.
Корреляционный момент:
!!! Если $K_{XY}\ne 0$, то горят, что между случайными величинами $X$ и $Y$ существует корреляционная связь. Если же $K_{XY}=0$, то говорят, что связь между величинами $X$ и $Y$ отсутствует.
Коэффициент корреляции:
!!! Отметим, что $\left|r_{XY}\right|\le 1$.
Пример задачи на нахождение числовых характеристик двумерной случайной величины
Случайная величина $(X,Y)$ задана следующей таблицей:

Рисунок 3.
Найти коэффициент $a$, математическое ожидание, дисперсию и среднее квадратическое отклонение для случайных величин $X$ и $Y$, а также корреляционный момент и коэффициент корреляции.
Решение: Для нахождения коэффициента $a$ используем условие нормированности для двумерной случайной величины
\[\sum\limits^m_{i=1}{\sum\limits^n_{j=1}{p_{ij}}}=1\]Найдем для начала сумму $\sum\limits^m_{i=1}{\sum\limits^n_{j=1}{p_{ij}}}$:
\[\sum\limits^m_{i=1}{\sum\limits^n_{j=1}{p_{ij}}}=0,6a+1,1a+0,3a+0,2a+0,6a+0,7a+0,65a+0,65a+0,2a=5a\]Следовательно: $5a=1,\ a=0,2$.
Получаем следующую таблицу распределения:

Рисунок 4.
Для удобства дальнейших вычислений найдем сначала $p_{y_i}=\sum\limits^n_{j=1}{p_{ij}}\ и\ $$p_{x_j}=\sum\limits^m_{i=1}{p_{ij}}$. Получим:
\[p_{x_1}=0,4,\ p_{x_2}=0,3,\ p_{x_3}=0,3,p_{y_1}=0,29,\ p_{y_2}=0,47,\ p_{y_3}=0,24\]Получим расширенную таблицу распределения случайной величины:
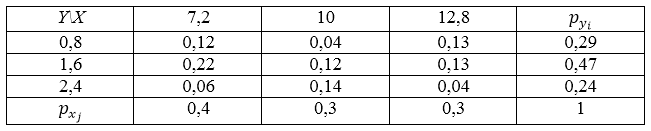
Рисунок 5.
Математическое ожидание:
\[M\left(X\right)=\sum\limits^3_{j=1}{{x_jp}_{x_j}}=7,2\cdot 0,4+10\cdot 0,3+12,8\cdot 0,3=9,72\] \[M\left(Y\right)=\sum\limits^3_{i=1}{{y_ip}_{y_i}}=0,8\cdot 0,29+1,6\cdot 0,47+2,4\cdot 0,24=1,56\]Дисперсия:
\[D\left(X\right)=\sum\limits^3_{j=1}{{x^2_jp}_{x_j}}-M^2\left(X\right)=20,736+30+49,152-94,4784=5,4096\] \[D\left(Y\right)=\sum\limits^3_{i=1}{{y^2_ip}_{y_i}}-M^2\left(Y\right)=0,1856+1,2032+1,3824-2,4336=0,3376\]Среднее квадратическое отклонение:
\[\sigma \left(X\right)=\sqrt{D(X)}=\sqrt{5,4096}=2,326\] \[\sigma \left(Y\right)=\sqrt{D(Y)}=\sqrt{0,3376}=0,581\]Корреляционный момент:
\[K_{XY}=M\left(XY\right)-M\left(X\right)M\left(Y\right)=15,152-15,1632=-0,0112\]Коэффициент корреляции:
\[r_{XY}=\frac{K_{XY}}{\sigma \left(X\right)\sigma \left(Y\right)}=\frac{-0,0112}{1,351406}=-0,008\]










