Основные сведения о координатной плоскости
Каждый объект (например, дом, место в зрительном зале, точка на карте) имеет свой упорядоченный адрес (координаты), который имеет числовое или буквенное обозначение.
Математики разработали модель, которая позволяет определять положение объекта и называется координатной плоскостью.
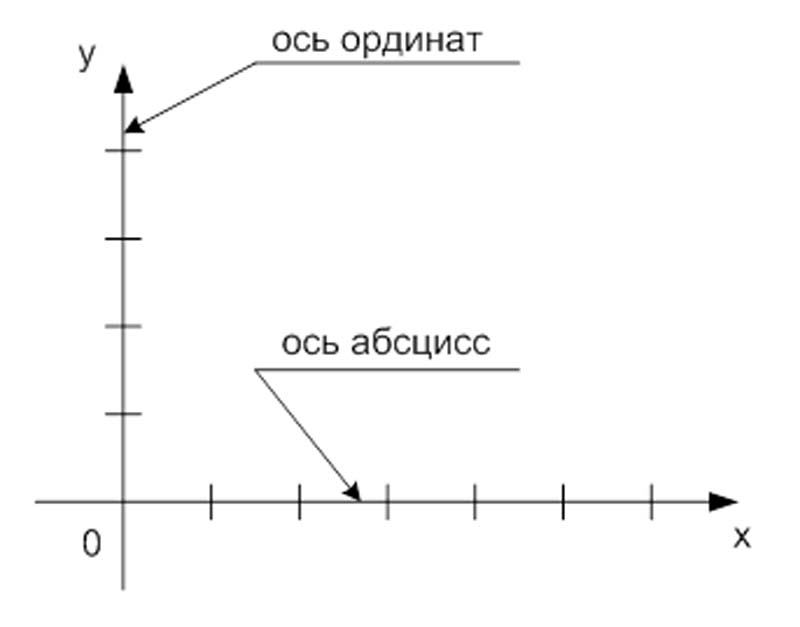
Чтобы построить координатную плоскость нужно провести $2$ перпендикулярные прямые, на конце которых указываются с помощью стрелок направления «вправо» и «вверх». На прямые наносятся деления, а точка пересечения прямых является нулевой отметкой для обеих шкал.
Две перпендикулярные оси х и у с делениями составляют прямоугольную, или декартовую, систему координат, которую предложил французский философ и математик Рене Декарт.
Координатная плоскость
Координаты точки
Точка на координатной плоскости определяется двумя координатами.
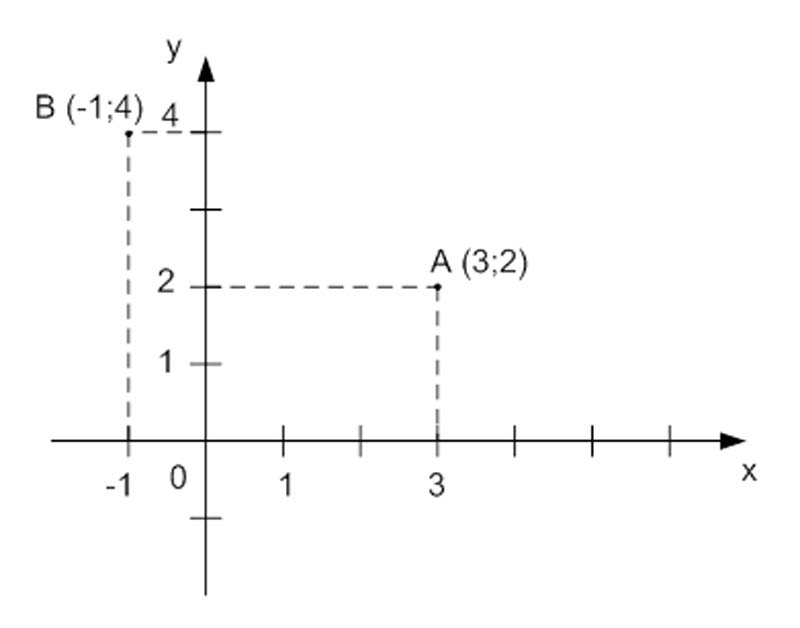
Чтобы определить координаты точки $A$ на координатной плоскости нужно через нее провести прямые, которые будут параллельны координатным осям (на рисунке выделены пунктирной линией). Пересечение прямой с осью абсцисс дает координату $x$ точки $A$, а пересечение с осью ординат дает координату у точки $A$. При записи координат точки сначала записывается координата $x$, а затем координата $y$.
Точка $A$ на рисунке имеет координаты $(3; 2)$, а точка $B (–1; 4)$.
Для нанесения точки на координатную плоскость действуют в обратном порядке.
Построение точки по заданным координатам
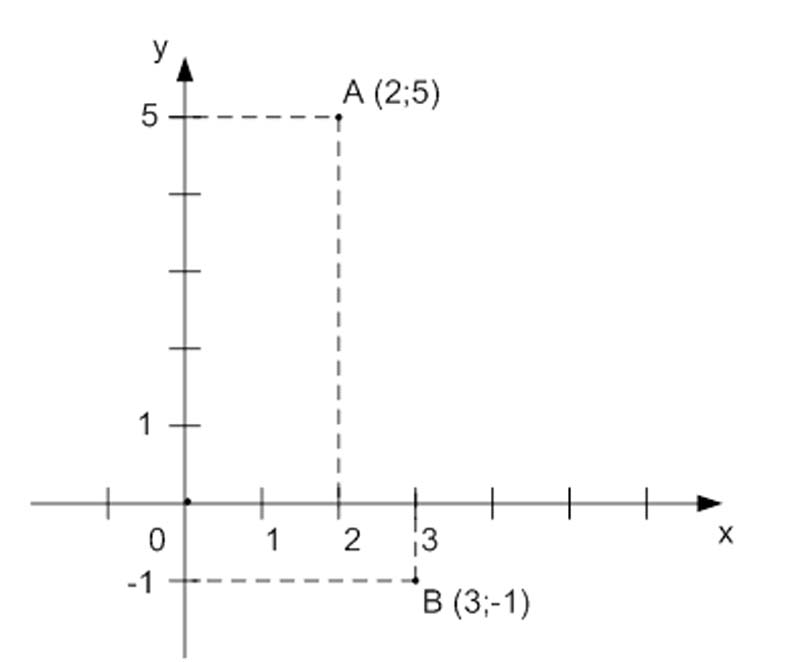
На координатной плоскости построить точки $A(2;5)$ и $B(3; –1).$
Решение.
Построение точки $A$:
- отложим число $2$ на оси $x$ и проведем перпендикулярную прямую;
- на оси у отложим число $5$ и проведем перпендикулярную оси $y$ прямую. На пересечении перпендикулярных прямых получим точку $A$ с координатами $(2; 5)$.
Построение точки $B$:
- отложим на оси $x$ число $3$ и проведем перпендикулярную оси х прямую;
- на оси $y$ отложим число $(–1)$ и проведем перпендикулярную оси $y$ прямую. На пересечении перпендикулярных прямых получим точку $B$ с координатами $(3; –1)$.
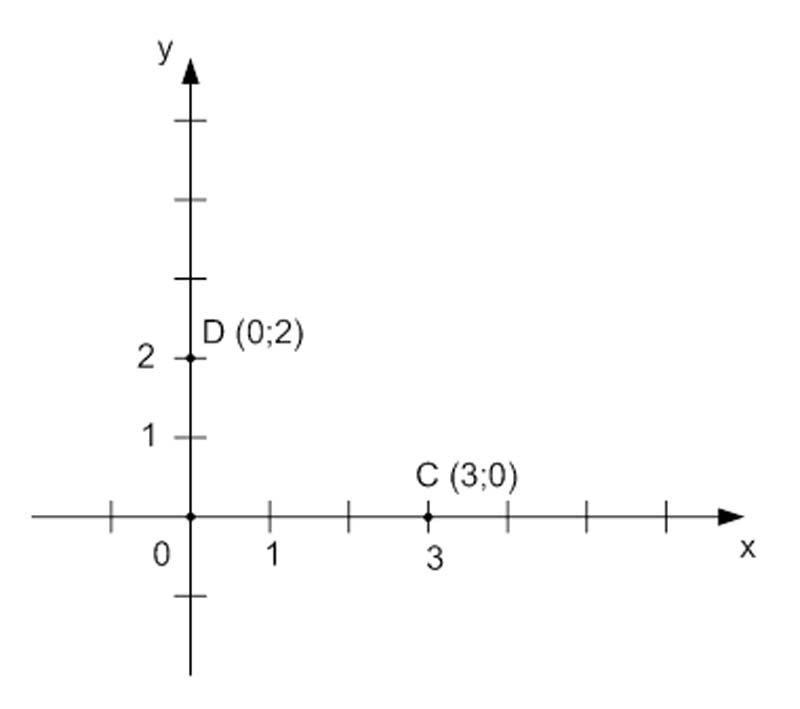
Построить на координатной плоскости точки с заданными координатами $C (3; 0)$ и $D(0; 2)$.
Решение.
Построение точки $C$:
- отложим число $3$ на оси $x$;
- координата $y$ равна нулю, значит точка $C$ будет лежать на оси $x$.
Построение точки $D$:
- отложим число $2$ на оси $y$;
- координата $x$ равна нулю, значит, точка $D$ будет лежать на оси $y$.
Следовательно, при координате $x=0$ точка будет лежать на оси $y$, а при координате $y=0$ точка будет лежать на оси $x$.
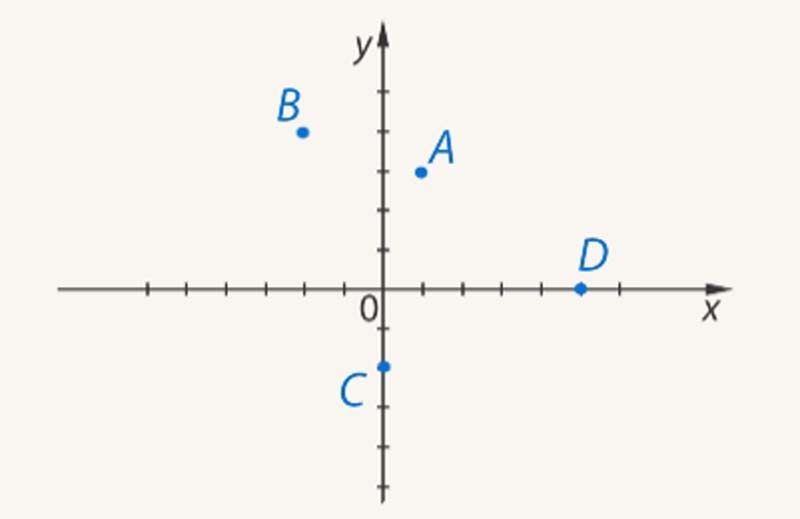
Определить координаты точек A, B, C, D.$
Решение.
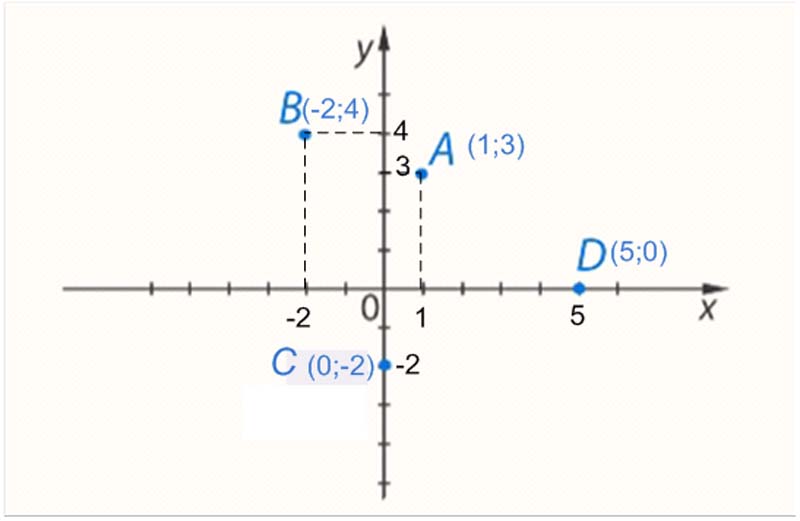
Определим координаты точки $A$. Для этого проведем через эту точку $2$ прямые, которые будут параллельными к координатным осям. Пересечение прямой с осью абсцисс дает координату $x$, пересечение прямой с осью ординат дает координату $y$. Таким образом, получаем, что точка $A (1; 3).$
Определим координаты точки $B$. Для этого проведем через эту точку $2$ прямые, которые будут параллельными к координатным осям. Пересечение прямой с осью абсцисс дает координату $x$, пересечение прямой с осью ординат дает координату $y$. Получаем, что точка $B (–2; 4).$
Определим координаты точки $C$. Т.к. она расположена на оси $y$, то координата $x$ этой точки равна нулю. Координата у равна $–2$. Таким образом, точка $C (0; –2)$.
Определим координаты точки $D$. Т.к. она находится на оси $x$, то координата $y$ равна нулю. Координата $x$ этой точки равна $–5$. Таким образом, точка $D (5; 0).$
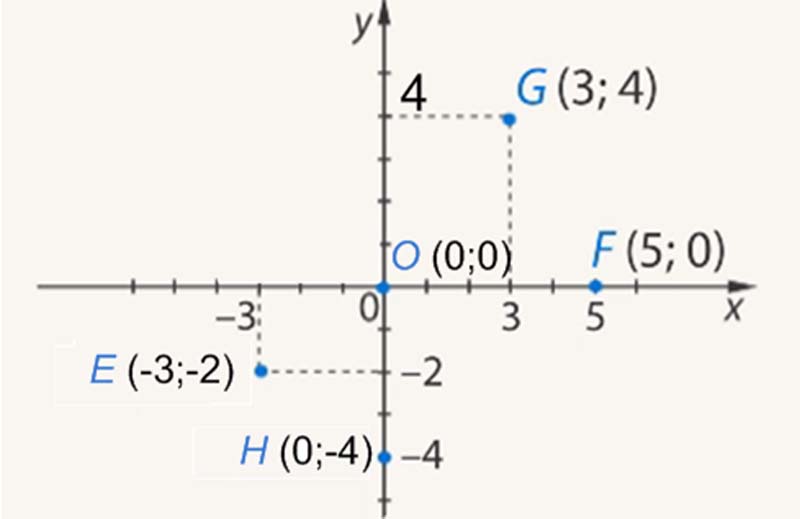
Построить точки $E(–3; –2), F(5; 0), G(3; 4), H(0; –4), O(0; 0).$
Решение.
Построение точки $E$:
- отложим число $(–3)$ на оси $x$ и проведем перпендикулярную прямую;
- на оси $y$ отложим число $(–2)$ и проведем перпендикулярную прямую к оси $y$;
- на пересечении перпендикулярных прямых получаем точку $E (–3; –2).$
Построение точки $F$:
- координата $y=0$, значит, точка лежит на оси $x$;
- отложим на оси $x$ число $5$ и получим точку $F(5; 0).$
Построение точки $G$:
- отложим число $3$ на оси $x$ и проведем перпендикулярную прямую к оси $x$;
- на оси $y$ отложим число $4$ и проведем перпендикулярную прямую к оси $y$;
- на пересечении перпендикулярных прямых получаем точку $G(3; 4).$
Построение точки $H$:
- координата $x=0$, значит, точка лежит на оси $y$;
- отложим на оси $y$ число $(–4)$ и получим точку $H(0; –4).$
Построение точки $O$:
- обе координаты точки равны нулю, значит, точка лежит одновременно и на оси $y$, и на оси $x$, следовательно является точкой пересечения обеих осей (началом координат).