
Если некоторая функция $g$ в каждой точке $х$ области значений обратимой функции $f$ принимает значение у такое, что $f(y) = x$, то говорят, что функция $g$ -- есть обратная к $f$ функция.
Пусть дан график некоторой обратимой функции $f$. Для того, чтобы построить график обратной функции, можно пользоваться следующим утверждением: график функции $f$ и обратной к ней функции $g$ будут симметричны относительно прямой, заданной уравнением $y = x$.
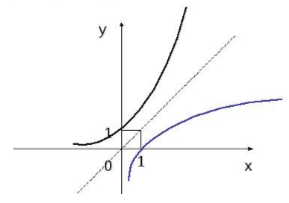
Рисунок 1. Обратные функции
Если функция $g$ является обратной к функции $f$, то функция $g$ будет являться обратимой функцией. А функция $f$ будет обратной к функции g. Обычно говорят, что две функции f и g взаимно обратные друг к другу.
Пусть $y = f(x)$ и $x = \varphi (y)$ -- взаимно обратные функции. Тогда если функция $y = f(x)$ имеет не равную нулю производную $f`(x)$, то обратная функция имеет производную $\varphi `(y)$.
$\phi '(y)=\frac{1}{f'(y)} $ или $x'_{y} =\frac{1}{y'_{x} } $
Поскольку $y = f(x)$ и $x = \varphi (y)$ -- взаимно обратные функции, то $x = \varphi (f(x))$. Применяя дифференцирование, получаем:
\[1=\phi '(y)f'(x)\]Найти производную функции
\[y=\sqrt[{n}]{x} \]Решение.
- Найдем функцию, обратную данной. Для этого выразим $х$ через $у$. \[y=f(x)=\sqrt[{n}]{x} \] \[y^{n} =\left(\sqrt[{n}]{x} \right)^{n} \] \[x=\phi (y)=y^{n} \]
- По теореме производной обратной функции: \[\left(\sqrt[{n}]{x} \right){{'} } =f'(x)=\frac{1}{\phi '(y)} =\frac{1}{\left(y^{n} \right){{'} } } =\frac{1}{ny^{n-1} } \]
- Заменим переменную $y$ \[\left(\sqrt[{n}]{x} \right){{'} } =\frac{1}{n\left(\sqrt[{n}]{x} \right)^{n-1} } \]
Найти производную функции
\[y=\ln x\]Решение.
- Найдем функцию, обратную данной. Для натурального логарифма обратной является функция $еy$. \[\left(\ln x\right){{'} } =f'(x)=\frac{1}{\phi '(y)} =\frac{1}{\left(e^{y} \right){{'} } } =\frac{1}{e^{\ln x} } \]
- Применим основное логарифмическое тождество \[\left(\ln x\right){{'} } =\frac{1}{e^{\ln x} } =\frac{1}{x} \]
Найти производную функции
\[y=\sqrt[{4}]{x^{2} -1} \]Решение.
- Найдем функцию, обратную данной. Для этого выразим $х$ через $у$. \[y=\sqrt[{4}]{x^{2} -1} \] \[y^{4} =x^{2} -1\] \[x=\phi (y)=\sqrt{y^{4} +1} \]
- Вычислим производную \[y'=f'(x)=\frac{1}{\phi '(x)} =\frac{1}{\left(\sqrt{y^{4} +1} \right){{'} } } \] \[y'=\frac{1}{\left(\sqrt{y^{4} +1} \right){{'} } } =\frac{\sqrt{y^{4} +1} }{\frac{1}{2} \cdot 4y^{3} } =\frac{\sqrt{y^{4} +1} }{2y^{3} } \]
Найти производную функции
\[y=\sqrt{2-\sqrt{x} } \]Решение.
- Найдем функцию, обратную данной. Для этого выразим $х$ через $у$. \[y=\sqrt{2-\sqrt{x} } \] \[y^{2} =2-\sqrt{x} \] \[\sqrt{x} =2-y^{2} \] \[x=\left(2-y^{2} \right)^{2} \]
- Вычислим производную \[\left(\sqrt{2-\sqrt{x} } \right){{'} } =\frac{1}{\phi '(x)} =\frac{1}{\left(2-y^{2} \right)^{2} {{'} } } \] \[\left(\sqrt{2-\sqrt{x} } \right){{'} } =\frac{1}{-2\left(2-y^{2} \right)2y} \]
- Упростим выражение \[\left(\sqrt{2-\sqrt{x} } \right){{'} } =\frac{1}{-4y\left(2-y^{2} \right)} \]
- Произведем замену $y$ \[\left(\sqrt{2-\sqrt{x} } \right){{'} } =\frac{1}{-4\sqrt{2-\sqrt{x} } \left(2-\left(\sqrt{2-\sqrt{x} } \right)^{2} \right)} =\frac{1}{-4\sqrt{2-\sqrt{x} } \left(2-2-\sqrt{x} \right)} =\frac{1}{-4\sqrt{2-\sqrt{x} } \left(-\sqrt{x} \right)} \]
- Упростим \[\left(\sqrt{2-\sqrt{x} } \right){{'} } =\frac{1}{-4\sqrt{2-\sqrt{x} } \left(-\sqrt{x} \right)} =\frac{1}{4\sqrt{x} \sqrt{2-\sqrt{x} } } \]










