Понятие корня $n$-ой степени
Пусть $a$ - действительное число и $n$ -- натуральное число больше единицы.
Корнем $n$-ой степени из числа $a$ называется такое действительное число $c$, что $c^n=a$.
Любое число $a
Если число $c$ - корень четной степени числа $a$, то $(-c)$ также корень четной степени числа $a$.
Арифметический корень
Действительное число $c\ge 0$ называется арифметическим корнем $n$-ой степени из действительного числа $a$, где $n$ -- натуральное число больше единицы, если $c^n=a$.
Каждое действительное число $a
Можно сформулировать следующую теорему:
Каждое число $a\ge 0$ при любом натуральном $n >1$ имеет единственный арифметический корень $n$-ой степени.
Свойства корней $n$-ой степени
-
Корень произведения равен произведению корней.
\[\sqrt[n]{ab}=\sqrt[n]{a}\sqrt[n]{b}\]где $a,b\ge 0$
-
Корень частного равен частному корней.
\[\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}\] - \[\sqrt[n]{\sqrt[k]{a}}=\sqrt[{nk}]{a}\]
- \[\sqrt[{nk}]{a^{mk}}=\sqrt[n]{a^m}\]
Иррациональные выражения
Рассмотрим пример задачи на упрощение иррациональных выражений.
Упростить выражение
\[\frac{\sqrt{x^3}+\sqrt{xy^2}-\sqrt{x^2y}-\sqrt{y^3}}{\sqrt[4]{y^5}+\sqrt[4]{x^4y}-\sqrt[4]{xy^4}-\sqrt[4]{x^5}}\]Решение.
Используя свойство корней 3, получим:
\[\frac{\sqrt{x^3}+\sqrt{xy^2}-\sqrt{x^2y}-\sqrt{y^3}}{\sqrt[4]{y^5}+\sqrt[4]{x^4y}-\sqrt[4]{xy^4}-\sqrt[4]{x^5}}=\frac{x\sqrt{x}+y\sqrt{x}-x\sqrt{y}-y\sqrt{y}}{y\sqrt[4]{y}+x\sqrt[4]{y}-y\sqrt[4]{x}-x\sqrt[4]{x}}=\] \[\frac{\sqrt{x}\left(x+y\right)-\sqrt{y}(x+y)}{\sqrt[4]{y}\left(y+x\right)-\sqrt[4]{x}(y+x)}=\frac{\sqrt{x}-\sqrt{y}}{\sqrt[4]{y}-\sqrt[4]{x}}=\frac{-\left(\sqrt[4]{y}-\sqrt[4]{x}\right)(\sqrt[4]{y}+\sqrt[4]{x})}{\sqrt[4]{y}-\sqrt[4]{x}}=-\sqrt[4]{y}-\sqrt[4]{x}\]Иррациональные уравнения
Рассмотрим задачи на решение иррациональных уравнений.
Решить уравнение $\sqrt[4]{2x+8}=2$
Решение.
Для решения данного уравнения воспользуемся теоремой
Теорема 2. Уравнение $\sqrt[{2n}]{f(x)} =g(x)$ равносильно системе
\[\left\{\begin{array}{l} {f(x)=g^{2n} (x),} \\ {g(x)\ge 0.} \end{array}\right. \]По теореме 1, получаем
\[\left\{ \begin{array}{c} {2x+8=2^4,} \\ {2x+8\ge 0.} \end{array} \right.\] \[\left\{ \begin{array}{c} {2x+8=16,} \\ {2x\ge -8.} \end{array} \right.\] \[\left\{ \begin{array}{c} {x=4,} \\ {x\ge -4.} \end{array} \right.\]Ответ: $4$.
Решить уравнение $\sqrt{2x-1}=x-2$
Найдем область определения:
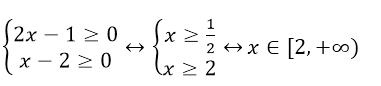
Рисунок 1.
Возведем обе части в квадрат:
\[2x-1=x^2-4x+4\] \[x^2-6x+5=0\] \[x=1-посторонний\ корень,\ x=5\]Ответ: $5$.
Иррациональные неравенства
Рассмотрим задачи на решение иррациональных неравенств.
Решить неравенство $\sqrt{{(x^2-2x+1)}^2} >4$
Решение.
Воспользовавшись свойством $\sqrt{x^2}=|x|$, получим
\[|x^2-2x+1| >4\]Данное неравенство равносильно совокупности
\[\left[ \begin{array}{c} {x^2-2x+1 >4,} \\ {x^2-2x+10,} \\ {x^2-2x+5Из первого неравенства получаем, что $x\in \left(-\infty ,-1\right)\left(3,+\infty \right)$.Так как дискриминант второго неравенства $D=4-20=-16
Ответ: $x\in \left(-\infty ,-1\right)\left(3,+\infty \right)$.
Решить неравенство $\sqrt{x^2-3x+2} >x+3$
Решение.
Данное неравенство равносильно совокупности двух систем.
-
Первая система:
\[\left\{ \begin{array}{c} {x+32} \end{array} \right. \end{array} \right.\] \[x\in (-\infty ,-3).\] -
Вторая система:
\[\left\{ \begin{array}{c} {x+3\ge 0,} \\ {x^2-3x+2\ge 0} \\ {x^2-3x+2 >{(x+3)}^2} \end{array} \right.\] \[\left\{ \begin{array}{c} {x\ge -3,} \\ \left[ \begin{array}{c} {x2} \end{array} \right. \\ {x^2-3x+2 >x^2+6x+9} \end{array} \right.\] \[\left\{ \begin{array}{c} {x\ge -3,} \\ \left[ \begin{array}{c} {x2} \end{array} \right. \\ {x
Ответ: $\left(-\infty ,-\frac{7}{9}\right)$












