Выпуклая и вогнутая функция
При исследовании заданной функции и построении ее графика встречаются понятия выпуклая и вогнутая функция.
Если функция $y=f(x)$ является дифференцируемой, тогда необходимо рассмотреть следующие определения.
Функция $y=f(x)$ называется выпуклой вниз на некотором интервале, если все точки графика этой функции расположены не ниже касательной, которая проведена к нему в любой точке рассматриваемого интервала.
Функция $y=f(x)$ называется выпуклой вверх на некотором интервале, если все точки графика этой функции расположены не выше касательной, которая проведена к нему в любой точке рассматриваемого интервала.
Схематическое изображение графиков выпуклой вниз (вогнутая функция) и выпуклой вверх (выпуклая) функций показано на рис.
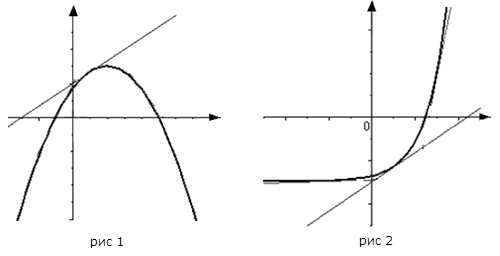
Рисунок 1. Графики выпуклой и вогнутой функции. Автор24 — интернет-биржа студенческих работ
Для нахождения интервалов выпуклости/вогнутости графика заданной функции необходимо использовать следующие теоремы.
Если $f''(x)$
Если $f''(x)>0$ для любой точки из рассматриваемого интервала, то график заданной функции на данном интервале направлен выпуклостью вниз.
Найти промежутки выпуклости и вогнутости функции $y=x^{5} $:
Решение:
Первая производная: $y'=5x^{4} $; вторая производная: $y''=20x^{3} $. Исследуя знак второй производной кривой, получаем, что $f''(x)0\, \, \forall x>0$. Следовательно, график направлен выпуклостью вверх при $x$0$.$, ,
Правило дождя
Для облегчения запоминания данных теорем можно использовать так называемое «правило дождя» (см. рис.).
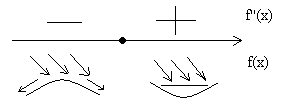
Рисунок 2. Правило дождя. Автор24 — интернет-биржа студенческих работ
«Правило дождя»:
- если $f''(x)$
- если $f''(x)>0$ (знак «+» соответствует киванию головы вверх-вниз, т.е. «да»), то лужа образуется, а значит, дождь падает во впадину (выпуклость вниз).
Отметим, что график может быть выпуклым или вогнутым на всей области определения заданной функции, а может только на отдельных промежутках. В таких случаях промежутки выпуклости и вогнутости сменяют друг друга.
Найти промежутки выпуклости/вогнутости графика заданной функции $y=x^{3} $.:
Решение:
$y'=3x^{2} $; вторая производная: $y''=6x$.
Изобразим на числовой оси (см. рис.).
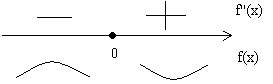
Рисунок 3. Изображение на числовой оси. Автор24 — интернет-биржа студенческих работ
Получаем, что $f''(x)$0\, \, \forall x>0$. Следовательно, график направлен выпуклостью вверх при $x$0$.
Точка перегиба - это такая точка графика выпуклой функции, которая разделяет промежутки выпуклости/вогнутости графика.
В примере 1 $x=0$ является точкой перегиба, так как при переходе через эту точку меняется поведение графика функции (в частности, с выпуклости на вогнутость).
Необходимое условие точки перегиба: В точке перегиба $(x_{0} ;y_{0} )$ вторая производная либо равна нулю, либо не существует.
Достаточное условие точки перегиба:
- $f'(x_{0} )$ непрерывна в окрестности заданной точки;
- $f''(x_{0} )=0$ или не существует в заданной точке;
- $f''(x)$ меняет знак на противоположный при переходе через заданную точку.
Учитывая все выше сказанное, составим алгоритм исследования выпуклости и вогнутости функции:
- нахождение первой производной $f'(x)$ заданной функции;
- нахождение второй производной $f''(x)$ заданной функции;
- определение точек, в которых $f''(x)$ равна нулю или не существует;
- исследование знака $f''(x)$ с помощью числовой прямой;
- определение промежутков выпуклости и вогнутости графика заданной функции;
- нахождение интервалов выпуклости и точки перегиба функции, если они существуют.
Найти точки перегиба графика заданной функции: $y=4x^{2} -3$.
Решение:
Первая производная: $y'=8x$; вторая производная: $y''=8$.
Изобразим на числовой оси (см. рис.).

Рисунок 4. Изображение на числовой оси. Автор24 — интернет-биржа студенческих работ
Получаем, что $f''(x)>0\, \, \forall x\in D_{y} $. Следовательно, график направлен выпуклостью вниз при любом $x$. Точек перегиба нет.
Найти точки перегиба графика заданной функции: $y=\frac{3}{x^{2} -1} $.
Решение:
Первая производная: $y'=\frac{0\cdot (x^{2} -1)-3\cdot 2x}{(x^{2} -1)^{2} } =-\frac{6x}{(x^{2} -1)^{2} } $.
Вторая производная: $y''=-\frac{6\cdot (x^{2} -1)^{2} -6x\cdot 2x\cdot 2\cdot (x^{2} -1)}{(x^{2} -1)^{4} } =-6\cdot \frac{x^{2} -1-4x}{(x^{2} -1)^{3} } $.
Вторая производная не существует при $x=\pm 1$.
\[\begin{array}{l} {y''=0:-6\cdot \frac{x^{2} -1-4x}{(x^{2} -1)^{3} } =0\Rightarrow x^{2} -4x-1=0} \\ {x^{2} -4x-1=0} \\ {D=16+4=20} \\ {x_{1} =\frac{4-\sqrt{20} }{2} =2-\sqrt{5} ;x_{2} =\frac{4+\sqrt{20} }{2} =2+\sqrt{5} } \end{array}\]Изобразим на числовой оси (см. рис.).

Рисунок 5. Изображение на числовой оси. Автор24 — интернет-биржа студенческих работ
Получаем, что:
- $f''(x)>0\, \, \forall x\in (-1;2-\sqrt{5} ]\bigcup (1;2+\sqrt{5} ]$,
- $f''(x)
Следовательно, график направлен выпуклостью вверх на промежутках $(-\infty ;-1)$, $[2-\sqrt{5} ;1)$ и $(1;+\infty )$, вниз на промежутках - $(-1;2-\sqrt{5} ]$ и $(1;2+\sqrt{5} ]$.












