Достаточно часто в курсе математического анализа можно встретить задание со следующей формулировкой: «исследовать функцию и построить график». Данная формулировка говорит сама за себя и разбивает задачу на два этапа:
- Этап 1: исследование функции;
- Этап 2: построение графика исследуемой функции.
Первый этап наиболее объемный и включает в себя отыскание областей определения и значений, экстремумов функции, точек перегиба графика и т.д.
Полный план исследования функции $y=f(x)$, предваряющий цель построение графика, имеет следующие пункты:
- Поиск области определения функции $D_{y} $ и области допустимых значений $E_{y} $ функции.
- Определение вида функции: четная, нечетная, общего вида.
- Определение точек пересечения графика функции с осями координат.
- Нахождение асимптот графика функции (вертикальные, наклонные, горизонтальные).
- Нахождение интервалов монотонности функции и точек экстремума.
- Нахождение промежутков выпуклости, вогнутости графика и точек перегиба.
Поиск области определения функции $D_{y} $ подразумевает нахождение интервалов, на которых данная функция существует (определена). Как правило, данная задача сводится к отысканию ОДЗ (область допустимых значений), на основании которых формируется $D_{y} $.
Найти область определения функции $y=\frac{x}{x-1} $.
Решение:
Найдем ОДЗ рассматриваемой функции, т.е. значения переменной, при которых знаменатель не обращается в ноль.
ОДЗ: $x-1\ne 0\Rightarrow x\ne 1$
Запишем область определения: $D_{y} =\{ x\in R|x\ne 1\} $.
Функция $y=f(x)$ является четной в случае, если выполняется следующее равенство $f(-x)=f(x)$ $\forall x\in D_{y} $.
Функция $y=f(x)$ является нечетной в случае, если выполняется следующее равенство $f(-x)=-f(x)$ $\forall x\in D_{y} $.
Функция, не являющаяся ни четной, ни нечетной, называется функцией общего вида.
Определить вид функций: 1) $y=\frac{x}{x-1} $, 2) $y=\frac{x^{2} }{x^{2} -1} $; 3) $y=\frac{x}{x^{2} -1} $.
Решение:
1) $y=\frac{x}{x-1} $
\[y(-x)=\frac{-x}{-x-1} =-\frac{x}{-x-1} \]$f(-x)\ne f(x);f(-x)\ne -f(x)$, следовательно, имеем функцию общего вида.
2) $y=\frac{x^{2} }{x^{2} -1} $
\[y(-x)=\frac{(-x)^{2} }{(-x)^{2} -1} =\frac{x^{2} }{x^{2} -1} \]$f(-x)=f(x)$, следовательно, имеем четную функцию.
3) $y=\frac{x}{x^{2} -1} $.
\[y(-x)=\frac{-x}{(-x)^{2} -1} =\frac{-x}{x^{2} -1} =-\frac{x}{x^{2} -1} \]$f(-x)\ne -f(x)$, следовательно, имеем нечетную функцию.
Определение точек пересечения графика функции с осями координат включает нахождение точек пересечения: с осью ОХ ($y=0$), с осью OY ($x=0$).
Найти точки пересечения с осями координат функции $y=\frac{x+2}{x-1} $.
Решение:
- с осью ОХ ($y=0$)
$\frac{x+2}{x-1} =0\Rightarrow x+2=0\Rightarrow x=-2$; получаем точку (-2;0)
- с осью ОY ($x=0$)
$y(0)=\frac{0+2}{0-1} =-2$, получаем точку (0;-2)
На основе результатов, полученных на этапе исследования функции, строится график. Иногда для построения графика функции недостаточно точек, полученных на первом этапе, тогда необходимо найти дополнительные точки.
Исследовать функцию и построить ее график: $y=x^{3} -6x^{2} +2x+1$.
Решение:
- Область определения: $D_{y} =\{ x|x\in R\} $.
- Область значений: $E_{y} =\{ y|y\in R\} $.
- Четность, нечетность функции:\[y(-x)=(-x)^{3} -6(-x)^{2} +2\cdot (-x)+1=-x^{3} -6x^{2} -2\cdot x+1\] \[y(-x)\ne -y(-x);y(-x)\ne y(x)\]
Функция общего вида, т.е. не является ни четной, ни нечетной.
4) Пересечение с осями координат:
-
с осью OY: $y(0)=0^{3} -6\cdot 0^{2} +2\cdot 0+1=1$, следовательно, график проходит через точку (0;1).
-
с осью OХ: $x^{3} -6x^{2} +2x+1=0$ (рациональных корней нет)
5) Асимптоты графика:
Вертикальных асимптот нет, так как $D_{y} =\{ x|x\in R\} $
Наклонные асимптоты будем искать в виде $y=kx+b$.
$k=\mathop{\lim }\limits_{x\to \infty } \frac{y(x)}{x} =\mathop{\lim }\limits_{x\to \infty } \frac{x^{3} -6x^{2} +2x+1}{x} =\infty $. Следовательно, наклонных асимптот нет.
6) Возрастание, убывание функции; экстремумы:
\[y'=(x^{3} -6x^{2} +2x+1)'=3x^{2} -12x+2\] \[\begin{array}{l} {y'=0\Rightarrow 3x^{2} -12x+2=0} \\ {D=144-24=120} \\ {x_{1,2} =\frac{12\pm \sqrt{120} }{6} } \end{array}\]Отметим точки на числовой оси, расставим знаки первой производной и отметим поведение функции:
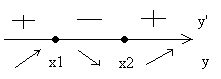
Рисунок 1.
Функция возрастает на $\left(-\infty ;\frac{12-\sqrt{120} }{6} \right]$ и $\left[\frac{12+\sqrt{120} }{6} ;\infty \right)$, убывает на $\left[\frac{12-\sqrt{120} }{6} ;\frac{12+\sqrt{120} }{6} \right]$.
$x=\frac{12-\sqrt{120} }{6} $ - точка максимума; $y\left(\frac{12-\sqrt{120} }{6} \right)=1,172$
$x=\frac{12+\sqrt{120} }{6} $ - точка минимума; $y\left(\frac{12+\sqrt{120} }{6} \right)=-23,172$
7) Выпуклость, вогнутость графика:
\[y'=(x^{3} -6x^{2} +2x+1)'=3x^{2} -12x+2\] \[\begin{array}{l} {y''=(3x^{2} -12x+2)'=6x-12} \\ {y''=0\Rightarrow 6x-12=0\Rightarrow x=2} \end{array}\]Отметим точки на числовой оси, расставим знаки второй производной и отметим поведение графика функции:
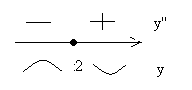
Рисунок 2.
График направлен выпуклостью вверх на $(-\infty ;2]$, вниз на $[2;\infty )$.
$x=2$ - точка перегиба
\[y(2)=2^{3} -6\cdot 2^{2} +2\cdot 2+1=8-24+4+1=-11\]8) График функции:
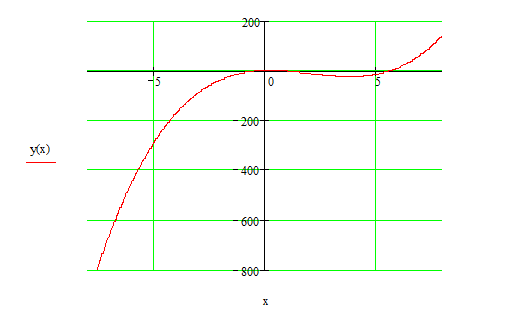
Рисунок 3.












