Понятие о геометрическом теле
Перед тем как ввести определение геометрического тела, введем следующие несколько вводных понятий.
Точка называется граничной для какой-либо фигуры, если близкие к ней точки как содержатся в фигуре, так и не содержатся в ней.
Границей какой-либо фигуры называется совокупность всех граничных точек для этой фигуры.
Точка называется внутренней для какой-либо фигуры, если она принадлежит этой фигуре, но при этом не является граничной для нее.
Фигура называется ограниченной, если ей можно вписать в какую-либо сферу пространства.
Фигура называется связной, если любые точки, принадлежащие этой фигуре, могут быть соединены какой-либо непрерывной линией, не выходящей за границы этой фигуры.
Введем теперь, наконец-то, непосредственно определение геометрического тела.
Геометрическое тело -- это фигура в пространстве, которая является ограниченной, связной и содержит все свои граничные точки.
Граница геометрического тела называется поверхностью этого геометрического тела.
Примерами геометрического тела могут служить многогранники и тела вращения. [/Определение]
Многогранником называется геометрическое тело в пространстве, которое ограниченно несколькими многоугольниками.
Примерами многогранников могут быть тетраэдр, куб, октаэдр, додекаэдр, икосаэдр и другие (рис. 1).
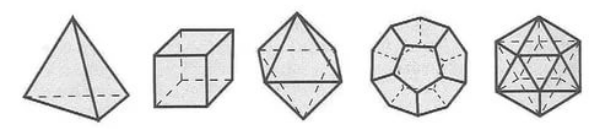
Рисунок 1. Примеры многогранников
Далее подробно рассмотрим тела вращения.
Поверхности вращения
Понятие тела вращения.
Поверхность, которая образуется путем вращения какой-либо произвольной линии вокруг прямой, называется поверхностью вращения.
При этом, прямая, вокруг которой вращается поверхность называется ос вращения и является осью симметрии для полученной поверхности.
Примерами поверхностей вращения могут быть цилиндр, конус, шар и другие (рис. 2).
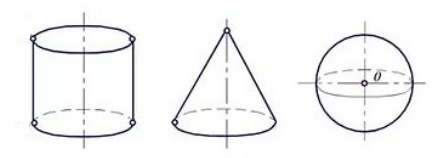
Рисунок 2. Примеры поверхностей вращения
Рассмотрим теперь тела вращения более подробно. Здесь мы не будем вдаваться в доказательства различных теорем.
Цилиндр.
Геометрическая фигура, образованная путем вращения прямоугольника вокруг одной из его сторон, называется цилиндром (рис. 3).
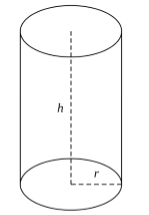
Рисунок 3. Цилиндр
Площадь поверхности цилиндра определяется следующим образом:
Площадь боковой поверхности цилиндра определяется как произведение длины окружности, ограничивающей основание цилиндра на его высоту, то есть
\[S_{бок}=2\pi rh\]Объем цилиндра определяется как произведение площади основания цилиндра на его высоту, то есть
\[V=\pi r^2h\]Конус.
Геометрическая фигура, образованная вращение прямоугольного треугольника вокруг своего катета, называется конусом (рис. 4).
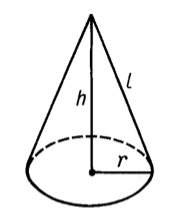
Рисунок 4. Конус
Площадь поверхности цилиндра определяется следующим образом:
Площадь боковой поверхности конуса определяется как половина произведения длины окружности, ограничивающей основание конуса на его образующую, то есть
\[S_{бок}=\pi lR\]Сфера.
Геометрическая фигура, образованная путем вращения полуокружности вокруг диаметра, называется сферой (рис. 5).
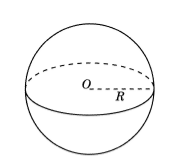
Рисунок 5.
Площадь сферы определяется следующей формулой:
Пример задачи
Найти площадь полной поверхности цилиндра и его объем, если радиус его основания равняется $7$ см, а высота в два раза больше диаметра основания.
Решение.
Найдем вначале высоту цилиндра. Так как высота в два раза больше диаметра, получим
\[h=2\cdot 2r=4r=28\ см\]Как мы знаем
\[S_{осн}=\pi r^2=49\pi \]По теореме 1
\[S_{бок}=2\pi rh=392\pi \]Тогда
\[S_{полн}=S_{бок}+2S_{осн}=392\pi +98\pi =490\pi \]По теореме 2
\[V=\pi r^2h=49\pi \cdot 28=1372\pi \]Ответ: $490\pi ,\ 1372\pi $












