Понятие многогранника
Многогранником называется геометрическое тело в пространстве, которое ограниченно несколькими многоугольниками. При этом многоугольники, из которых состоят многогранники, называют гранями многогранника, стороны многоугольников – сторонами многогранника, а вершины многоугольников – вершинами многогранника.
Если многогранник всегда будет лежать по одну сторону от любой плоскости его граней, то многогранник называется выпуклым (рис. 1).
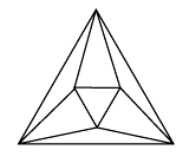
Рисунок 1. Выпукклый многогранник
Если многогранник лежит по разные стороны хотя бы одной плоскости его грани, то многогранник называется невыпуклым (рис. 2).
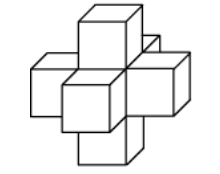
Рисунок 2. Невыпуклый многогранник
Многогранник называется правильным, если он удовлетворяет следующим условиям:
- Многогранник является выпуклым;
- Все грани многогранника правильные, равные между собой многоугольники;
- В каждой вершине многогранника сходится одинаковое число ребер.
Рассмотрим далее примеры классических многогранников в курсе стереометрии.
Тетраэдр
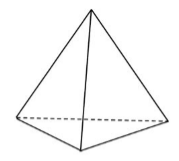
Геометрическая фигура в пространстве, составленная из треугольника, вершины которого соединены с точкой, не лежащей в плоскости, содержащей треугольник, называется тетраэдром (рис. 3).
 Тетраэдр">
Тетраэдр">
Рисунок 3. Тетраэдр
Таким образом, гранями тетраэдра являются $4$ треугольника.
Параллелепипед
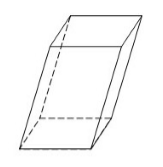
Геометрическая фигура, образованная двумя равными параллелограммами, лежащими в параллельных плоскостях, а их вершины соединены между собой так, что между параллельными плоскостями образуются две пары параллелограммов, лежащих в параллельных плоскостях, называется параллелепипедом (рис. 4).
 Параллелепипед">
Параллелепипед">
Рисунок 4. Параллелепипед
Параллелограммы, из которых составлен параллелепипед, называются гранями параллелепипеда, стороны параллелограммов – сторонами параллелепипеда, а вершины параллелограммов – вершинами параллелепипеда.
Призма
Геометрическая фигура, образованная двумя равными n-угольниками, лежащими в параллельных плоскостях, вершины которых соединены между собой так, что соответствующая вершина первого n-угольника соединена с соответствующей вершиной второго n-уголника, называется призмой (рис. 5).
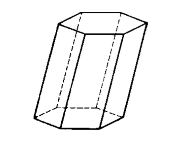
Рисунок 5. Призма
Параллельные $n$-уголники называются основаниями призмы, параллелограммы их соединяющие – боковыми гранями, стороны параллелограммов – сторонами призмы, а вершины $n$-угольников – вершинами призмы.
Пирамида
Геометрическая фигура, образованная многоугольником и точкой, не лежащей в плоскости, содержащей этот многоугольник, соединенной со всеми вершинами многоугольника называется пирамидой (рис. 6).
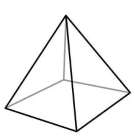
Многоугольник, из которого составлена пирамида, называется основанием пирамиды, получаемые при соединение с точкой треугольники – боковыми гранями пирамиды, стороны треугольников – сторонами пирамиды, а общая для всех треугольников точка– вершиной пирамиды.
Другие примеры многогранников
Также иногда рассматриваются такие многогранники как октаэдр, додекаэдр и икосаэдр. Приведем их иллюстрации (рис. 7).
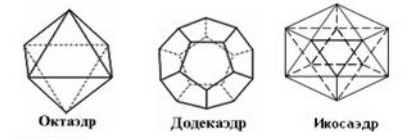
Рисунок 7.
Пример задачи
Здесь мы предложим вам практическое задание.
На рисунке 8 приведены развертки различных правильных многогранников. Перерисуйте их на картонной бумаге (дополняя краешками для склеивания), вырежьте и склейте из них фигуры.
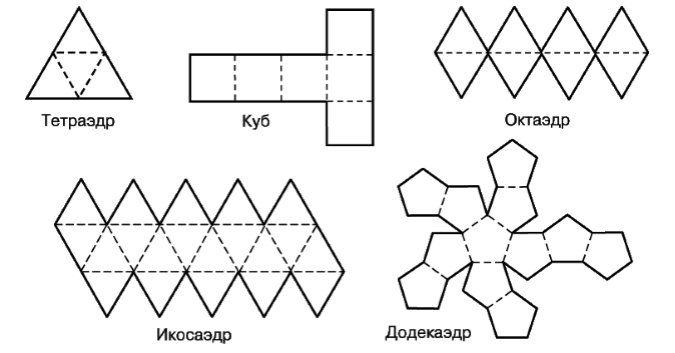
Рисунок 8.












