
Криволинейные интегралы являются обобщением определенного интеграла в случае, когда область интегрирования это некоторая кривая.
Криволинейный интеграл первого рода
 Криволинейный интеграл">
Криволинейный интеграл">
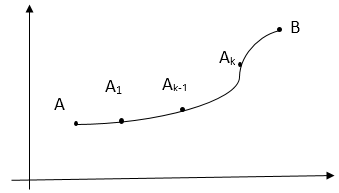
Пускай на прямой AB задано функцию $f\left(x,y\right).$ Разбив эту кривую на n частей и выбрав на каждой из частей произвольную точку $M_k\left({\xi }_k,{\eta }_k\right),$ найдем значение $f\left({\xi }_k,{\eta }_k\right),$ и составим интегральную сумму
$I_n=\sum\limits^n_{k=1}{f\left({\xi }_k,{\eta }_k\right)\vartriangle l_k,}$где $\vartriangle l_k-$длина k-ой части кривой.
Найдем
Если при $\lambda \to 0\ \left(\lambda ={\mathop{max}_{k} \left\{\vartriangle l_k\right\}\ }\right)$ эта граница существует и не зависит от способа разбития кривой AB на части и выбора точки $M_k$, то его называют криволинейным интегралом первого рода от функции $f\left(x,y\right)$ по кривой AB и обозначают
\[\int\limits_{AB}{f\left(x,y\right)dl.}\]Значит,
\[\int\limits_{AB}{f\left(x,y\right)dl=}{\mathop{lim}_{\lambda \to 0} \sum\limits^n_{k=1}{f\left({\xi }_k,{\eta }_k\right)\vartriangle l_k}\ }\]В этом случае функцию $f\left(x,y\right)$ называют интегрированной вдоль кривой AB, а кривую AB -- контуром интегрирования, A -- начальная, а B -- конечной точками интегрирования.
Свойства интеграла первого рода:
- $\int\nolimits_{AB}{f\left(x,y\right)dl=\int\nolimits_{BA}{f\left(x,y\right)dl.}}$
- Если $f\left(x,y\right)\ge 0$ на отрезке AB, то криволинейный интеграл $\int\limits_{AB}{f\left(x,y\right)dl}$ не отрицательный на отрезке AB.
- $\int\nolimits_{AB}{C\ f\left(x,y\right)dl=C\ \int\nolimits_{AB}{f\left(x,y\right)dl.}}$
- $\int\nolimits_{AB}{\left(f\left(x,y\right)\mp g\left(x,y\right)\right)dl=\int\nolimits_{AB}{f\left(x,y\right)dl\mp \int\nolimits_{AB}{g\left(x,y\right)dl.}}}$
- Если кривую AB разбить точкой C на части, то \[\int\limits_{AB}{f\left(x,y\right)dl=\int\limits_{AС}{f\left(x,y\right)dl+\int\limits_{СB}{f\left(x,y\right)dl.\ }}}\]
Криволинейный интеграл второго рода
Пускай на плоской кривой AB задано непрерывную функцию $f\left(x,y\right).$ Разобьем кривую AB точками $A=A0, A1, A2, \dots , An=B$ на $n$ частей. На каждом промежутке $Ak-1Ak$ выберем произвольную точку $M_k\left({\xi }_k,{\eta }_k\right)$ и составим сумму $\sum\limits^n_{k=1}{f\left({\xi }_k,{\eta }_k\right)\vartriangle x_k},$ где $\vartriangle x_k-$проекция вектора $\overline{A_{k-1}A_k}$ на ось Ox. Эту сумму называют интегральной. Найдем ее границу:
\[{\mathop{lim}_{\lambda \to 0} \sum\limits^n_{k=1}{f\left({\xi }_k,{\eta }_k\right)\vartriangle x_k,\ \ \ \ \lambda ={\mathop{max}_{k} \left\{\vartriangle l_k\right\}.\ }}\ }\]Если при $\lambda \to 0\ \left(\lambda ={\mathop{max}_{k} \left\{\vartriangle l_k\right\}\ }\right)$ граница интегрированной суммы существует и не зависит от способа разбития кривой AB на части и от выбора точки Mk , то его называют криволинейным интегралом от функции $f\left(x,y\right)$ по абсциссе $x$ вдоль кривой AB и обозначают $\int\nolimits_{AB}{f\left(x,y\right)dx.}$
Таким образом
\[\int\limits_{AB}{f\left(x,y\right)dx={\mathop{lim}_{\lambda \to 0} \sum\limits^n_{k=1}{f\left({\xi }_k,{\eta }_k\right)\vartriangle x_k}\ }.}\]Свойства криволинейного интеграла второго рода:
- $\int\nolimits_{AB}{f\left(x,y\right)dx=-\int\nolimits_{BA}{f\left(x,y\right)dx.}}$
- $\int\nolimits_{AB}{\left(f\left(x,y\right)\mp g\left(x,y\right)\right)dx=\int\nolimits_{AB}{f\left(x,y\right)dx\mp \int\nolimits_{AB}{g\left(x,y\right)dx.}}}$
- $\int\nolimits_{AB}{C\ f\left(x,y\right)dx=C\ \int\nolimits_{AB}{f\left(x,y\right)dx.}}$
- $\int\nolimits_{AB}{f\left(x,y\right)dx=\int\nolimits_{AС}{f\left(x,y\right)dx+\int\nolimits_{СB}{f\left(x,y\right)dx.\ }}}$
- $\int\nolimits_{AB}{f\left(x,y\right)dx=0,}$ когда $AB\parallel OY; \ \ \int\nolimits_{AB}{f\left(x,y\right)dy=0,}$ когда $AB\parallel OX$
Условия независимости криволинейного интеграла от пути интегрирования.
Для того, что б в связной области D, криволинейный интеграл $\int\limits_{AB}{P\left(x,y\right)dx+Q\left(x,y\right)dy}$ независим от пути AB. Необходимо и достаточно, что бы интеграл по замкнутому контуру в этой области равнялся нулю:
\[\int\limits_{AB}{P\left(x,y\right)dx+Q\left(x,y\right)dy}=0.\]Вычислить интеграл
$I=\ \int\limits_{AB}{2xy\ dx+x^2dy}$ от т. А(0,0) до точки В(1,1).
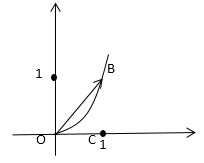
- Найдем по прямой$\ y=x$, $dy=dx$ \[I=\ \int\limits^1_0{2xx\ dx+x^2dx=}\int\limits^1_0{3x^2dx=}{\left.\frac{3x^3}{3}\right|}^1_0=1.\]
- Найдем по ветке параболы $y=x^2$, $dy=2x\ dx$ \[I=\ \int\limits^1_0{2x^3\ dx+{2x}^3dx=}\int\limits^1_0{4x^3dx=}{\left.\frac{4x^4}{4}\right|}^1_0=1.\]
- Найдем по контуру ОСВ: \[I=\int\limits_{OCB}{P\ dx+Qdy=\int\limits_{OCB}{2xy\ dx+x^2dy=\int\limits_{OC}{\left(2xy\ dx+x^2dy\right)}+}}+\int\limits_{CB}{\left(2xy\ dx+x^2dy\right)}\]
- Найдем для ОС -- $y=0$, $dy=0$ и подставим в формулу: \[\int\limits_{OC}{2xy\ dx+x^2dy=0}\]
- Найдем для СВ -- $x=1,\ \ dx=0$ и подставим в формулу: \[\int\limits_{CB}{2xy\ dx+x^2dy=1\int\limits^1_0{dy}=1}.\]
Пример хорошо показывает независимость криволинейного интеграла от пути интегрирования. В данном примере мы выбрали три разных пути, и при вычислении интеграла во всех случаях получили один и тот же ответ.
Для работы с криволинейными интегралами не менее важной есть следующая теорема.
Если в односвязной области D функции $P\left(x,y\right)$ и $Q\left(x,y\right)$ и их производные $\frac{\partial P}{\partial y}$ и $\frac{\partial Q}{\partial x}$ непрерывные, то для того что бы интеграл по замкнутому контуру в этой области был равен нулю необходимо и достаточно что бы выполнялось равенство:
$\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}$во всех точках этой области.
Связь между криволинейным интегралом первого и второго рода
С помощью определения интегралов первого и второго рода и определения интеграла, очень просто показать связь между криволинейным интегралом первого и криволинейным интегралом второго рода.
От криволинейного интеграла второго рода очень просто перейти до криволинейного интеграла первого рода. Переход между ними выражается формулой:
\[\int\limits_{AB}{P\left(x,y\right)dx+Q\left(x,y\right)dy}=\int\limits_{AB}{Pdl{cos \alpha \ }+Qdl{cos \beta \ }}\]









