Криволинейные интегралы являются обобщением определенного интеграла в случае, когда область интегрирования это некоторая кривая.
Криволинейный интеграл первого рода
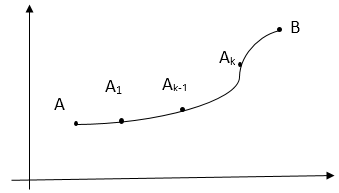Криволинейный интеграл">
Если на прямой AB задано функцию $f\left(x,y\right).$
Разбив эту кривую на n частей и выбрав на каждой из частей произвольную точку $M_k\left({\xi }_k,{\eta }_k\right),$ найдем значение $f\left({\xi }_k,{\eta }_k\right)$ и составим интегральную сумму
$I_n=\sum\limits^n_{k=1}{f\left({\xi }_k,{\eta }_k\right)\vartriangle l_k,}$ где $\vartriangle l_k-$длина k-ой части кривой.
Найдем
Если при $\lambda \to 0\ \left(\lambda ={\mathop{max}_{k} \left\{\vartriangle l_k\right\}\ }\right)$ эта граница существует и не зависит от способа разбития кривой AB на части и выбора точки $M_k$, то его называют криволинейным интегралом первого рода от функции $f\left(x,y\right)$ по кривой AB и обозначают
\[\int\limits_{AB}{f\left(x,y\right)dl.}\]Значит,
\[\int\limits_{AB}{f\left(x,y\right)dl=}{\mathop{lim}_{\lambda \to 0} \sum\limits^n_{k=1}{f\left({\xi }_k,{\eta }_k\right)\vartriangle l_k}\ }\]В этом случае функцию $f\left(x,y\right)$ называют интегрированной вдоль кривой AB, а кривую AB -- контуром интегрирования, A -- начальная, а B -- конечной точками интегрирования.
Пускай кривую AB -- задано параметрическими уравнениями:
$x=x\left(t\right),\ \ y=y\left(t\right),\ \ \ \ t\in \left[\alpha ;\beta \right],$где функция $x=x\left(t\right),\ \ y=y\left(t\right)$ и её производные $x=x'\left(t\right),\ \ y=y'\left(t\right)$ -- непрерывны на отрезке $\left[\alpha ;\beta \right]$.
Рассмотрим правую часть уравнения:
$\int\limits_{AB}{f\left(x,y\right)dl=}{\mathop{lim}_{\lambda \to 0} \sum\limits^n_{k=1}{f\left({\xi }_k,{\eta }_k\right)\vartriangle l_k}\ }$где прирост $\vartriangle l_k$ найдем по формуле:
$l=\int\limits^{\beta }_{\alpha }{\sqrt{{\left(x'\left(t\right)\right)}^2+{\left(y'\left(t\right)\right)}^2}dt}$а потом воспользуемся теоремой о среднем и получим:
$\vartriangle l_k=\int\limits^{t_k}_{t_{k-1}}{\sqrt{{\left(x'\left(t\right)\right)}^2+{\left(y'\left(t\right)\right)}^2}dt}=\sqrt{{\left(x'\left({\tau }_k\right)\right)}^2+{\left(y'\left({\tau }_k\right)\right)}^2}\triangle t_k$где ${\tau }_k\in [t_{k-1};t_k]$.
На каждой промежутке точки Ak-1Ak вместо точки $M_k$выберем точку $\overline{M_k}\left(\overline{{\xi }_k},\overline{{\eta }_k}\right)$ где $\overline{{\xi }_k}=x({\tau }_k)$, $\overline{{\eta }_k}=y\left({\tau }_k\right).$ Тогда:
\[\sum\limits^n_{k=1}{f\left(\overline{{\xi }_k},\overline{{\eta }_k}\right)\vartriangle l_k}=\sum\limits^n_{k=1}{f\left(x({\tau }_k),y\left({\tau }_k\right)\right)\sqrt{{\left(x'\left({\tau }_k\right)\right)}^2+{\left(y'\left({\tau }_k\right)\right)}^2}\triangle t_k}.0\]
Правая часть этого равенства есть интегральной суммой для непрерывной функции
$f\left(x\left(t\right),y\left(t\right)\ \right)\sqrt{{\left(x'\left(t\right)\right)}^2+{\left(y'\left(t\right)\right)}^2}$на отрезке $\left[\alpha ;\beta \right].$ Предел этой суммы при $\lambda \to 0\ \left(\lambda ={\mathop{max}_{k} \left\{\vartriangle l_k\right\}\ }\right)$ это определенный интеграл:
\[\int\limits^{\beta }_{\alpha }{f\left(x\left(t\right),y\left(t\right)\ \right)\sqrt{{\left(x'\left(t\right)\right)}^2+{\left(y'\left(t\right)\right)}^2}dt}\]Криволинейный интеграл второго рода
Пускай на плоской кривой AB задано непрерывную функцию $f\left(x,y\right).$ Разобьем кривую AB точками $A=A0, A1, A2, \dots, An=B$ на $n$ частей. На каждом промежутке $Ak-1Ak$ выберем произвольную точку $M_k\left({\xi }_k,{\eta }_k\right)$ и составим сумму $\sum\limits^n_{k=1}{f\left({\xi }_k,{\eta }_k\right)\vartriangle x_k},$ где $\vartriangle x_k-$проекция вектора $\overline{A_{k-1}A_k}$ на ось Ox. Эту сумму называют интегральной. Найдем ее границу:
\[{\mathop{lim}_{\lambda \to 0} \sum\limits^n_{k=1}{f\left({\xi }_k,{\eta }_k\right)\vartriangle x_k,\ \ \ \ \lambda ={\mathop{max}_{k} \left\{\vartriangle l_k\right\}.\ }}\ }\]Если при $\lambda \to 0\ \left(\lambda ={\mathop{max}_{k} \left\{\vartriangle l_k\right\}\ }\right)$ граница интегрированной суммы существует и не зависит от способа разбития кривой AB на части и от выбора точки Mk , то его называют криволинейным интегралом от функции $f\left(x,y\right)$ по абсциссе $x$ вдоль кривой AB и обозначают $\int\nolimits_{AB}{f\left(x,y\right)dx.}$
Таким образом
\[\int\limits_{AB}{f\left(x,y\right)dx={\mathop{lim}_{\lambda \to 0} \sum\limits^n_{k=1}{f\left({\xi }_k,{\eta }_k\right)\vartriangle x_k}\ }.}\]Пускай кривую AB -- задано параметрическими уравнениями:
$x=x\left(t\right),\ \ y=y\left(t\right),\ \ \ \ t\in \left[\alpha ;\beta \right],$где функция $x=x\left(t\right),\ \ y=y\left(t\right)$ и её производные $x=x'\left(t\right),\ \ y=y'\left(t\right)$ -- непрерывны на отрезке $\left[\alpha ;\beta \right]$.
Рассмотрим правую часть уравнения:
$\int\limits_{AB}{f\left(x,y\right)dx={\mathop{lim}_{\lambda \to 0} \sum\limits^n_{k=1}{f\left({\xi }_k,{\eta }_k\right)\vartriangle x_k}\ }}$
Прирост $\vartriangle x_k$ подсчитаем по формуле Лагранжа:
\[\vartriangle x_k=\ x\left(t_k\right)-x\left(t_{k-1}\right)=x'\left({\tau }_k\right)\left(t_k-t_{k-1}\right)=x'\left({\tau }_k\right)\vartriangle t_k.\]На каждой промежутке точки Ak-1Ak вместо точки $M_k$выберем точку $\overline{M_k}\left(\overline{{\xi }_k},\overline{{\eta }_k}\right)$ где $\overline{{\xi }_k}=x({\tau }_k)$, $\overline{{\eta }_k}=y\left({\tau }_k\right).$ Тогда:
\[\sum\limits^n_{k=1}{f\left(\overline{{\xi }_k},\overline{{\eta }_k}\right)\vartriangle x_k=}\sum\limits^n_{k=1}{f\left(x({\tau }_k),y({\tau }_k)\right)x'\left({\tau }_k\right)\vartriangle t_k}.\]Правая часть этого равенства есть интегральной суммой для непрерывной функции $f\left(x(t),y(t)\right)x'\left(t\right)$ на отрезке $\left[\alpha ;\beta \right].$
Предел этой суммы при $\lambda \to 0\ \left(\lambda ={\mathop{max}_{k} \left\{\vartriangle l_k\right\}\ }\right)$ это определенный интеграл:
\[\int\limits^{\beta }_{\alpha }{f\left(x\left(t\right),y\left(t\right)\right)x'\left(t\right)dt}\]Найти интеграл
$I=\int\limits_{AB}{x^2dx+y^2dy,}$где $AB$ -- отрезок, что соединяет точки $A(1;2)$ и $B(3;-4)$.
Напишем уравнение прямой$\ AB$:
\[\frac{x-1}{3-1}=\frac{y-2}{-4-2},\ \ \ \ \ \frac{x-1}{2}=\frac{y-2}{-6},\] \[y=-3x+5,\ \ \ \ dy--3dx.\]Тогда по формуле криволинейного интеграла:
\[I=\int\limits^3_1{{(x}^2dx+{\left(-3x+5\right)}^2(-3dx))=\int\limits^3_1{{(x}^2+(9x^2-30x+25)(-3))dx=}}\] \[\int\limits^3_1{{(90x-26x}^2-75)dx{=\left.\left(90\frac{x^2}{2}-26\frac{x^3}{3}-75x\right)\right|}^3_1=}\] \[=45\left(9-1\right)-\frac{26}{3}\left(27-1\right)-75\left(3-1\right)=-\frac{46}{3}.\]
