Обозначение и геометрический смысл двойного интеграла
Двойной интеграл (ДИ) от функции $f\left(x,y\right)$ по области $D$ обозначают $I=\iint \limits _{D}f\left(x,y\right)\cdot dS $ или $I=\iint \limits _{D}f\left(x,y\right)\cdot dx\cdot dy $. При этом область $D$ называется областью интегрирования, $x$ и $y$ -- переменными интегрирования, а $dS=dx\cdot dy$ -- элементом площади.
Геометрический смысл ДИ от непрерывной неотрицательной функции состоит в том, что он дает точное значение объема некоторого криволинейного цилиндра, то есть объема тела, ограниченного сверху графиком функции $f\left(x,y\right)$, по бокам -- цилиндрической поверхностью (направляющая -- линия $L$, образующие параллельны оси $Oz$), а снизу -- областью $D$, лежащей в координатной плоскости $xOy$.
Вычисление двойного интеграла
Статья: Двойной интеграл, вычисление двойного интеграла
С целью вычисления ДИ осуществляют его приведение к повторному. Вследствие этого результат удается получить путем последовательного вычисления двух обычных определенных интегралов.
Рассмотрим объем определенного криволинейного цилиндра $V=\iint \limits _{D}f\left(x,y\right)\cdot dx\cdot dy $, ограничившись простым случаем. Пусть функция $f\left(x,y\right)>0$ положительна в пределах области $D$. Сама область $D$ ограничена на координатной плоскости $xOy$ прямыми линиями $x=a$ и $x=b$, где $ a
Полученный результат представляет собой приведение ДИ к повторному для произвольной непрерывной функции $f\left(x,y\right)$ при условии, что область $D$ является правильной в направлении оси $Oy$.
Правильная в направлении оси $Oy$ область $D$ должна быть образована непрерывными кривыми $y=\vartheta _{1} \left(x\right)$ и $y=\vartheta _{2} \left(x\right)$, а также прямыми $x=a$ и $x=b$, которые удовлетворяют условиям $\vartheta _{1} \left(x\right)\le \vartheta _{2} \left(x\right)$ и $a
В повторном интеграле сначала вычисляют внутренний интеграл, в котором интегрирования выполняется по $y$, а $x$ предполагается постоянным. В результате будет получена функция от $x$, которую нужно проинтегрировать по $x$ в пределах от $a$ к $b$.
Допустимо также рассматривать область $D$ правильной в направлении оси $Ox$.
Правильная в направлении оси $Ox$ область $D$ должна быть образована непрерывными кривыми $x=\psi _{1} \left(y\right)$ и $x=\psi _{2} \left(y\right)$, а также прямыми $y=c$ и $y=d$, которые удовлетворяют условиям $\psi _{1} \left(y\right)\le \psi _{2} \left(y\right)$ и $c Если область $D$ не является правильной в направлении ни одной из осей, то ее надо разбить на конечное количество правильных подобластей линиями, параллельными осям координат. При этом интеграл по области $D$ будет равным сумме интегралов по каждой из подобластей. То же самое надо сделать, если область $D$ является правильной, но ее границы состоят из нескольких участков, которые имеют разные уравнения. Предположим, что в координатной плоскости $xOy$ задана замкнутая область $D$, ограниченная линией $L$. В этой области задана непрерывная функция $f\left(x,y\right)$, для которой существует ДИ $\iint \limits _{D}f\left(x,y\right)\cdot dx\cdot dy $. Пусть при вычислении ДИ оказалось целесообразным перейти к новым переменным $u$ и $v$ с помощью формул $x=\vartheta \left(u,v\right)$ и $y=\psi \left(u,v\right)$. Предположим, что указанными формулами устанавливается взаимно однозначное соответствие между точками $P\left(x,y\right)$ заданной области $D$ и точками $P^{*} \left(u,v\right)$ некоторой области $D^{*} $. Предполагаем, что функции $\vartheta \left(u,v\right)$ и $\psi \left(u,v\right)$ непрерывны и имеют непрерывные частные производные в области $D^{*} $. Формула замены переменной в ДИ имеет вид: Здесь $J\left(u,v\right)=\left|\begin{array}{cc} {\frac{\partial \vartheta }{\partial u} } & {\frac{\partial \vartheta }{\partial v} } \\ {\frac{\partial \psi }{\partial u} } & {\frac{\partial \psi }{\partial v} } \end{array}\right|$ -- функциональный определитель (якобиан) функций $\vartheta \left(u,v\right)$ и $\psi \left(u,v\right)$. ДИ в полярных координатах -- частный случай замены переменных. Перейдем к полярным координатам $\rho $ и $\phi $, учитывая, что они связаны с прямоугольными координатами $x$ и $y$ с помощью формул $x=\rho \cdot \cos \phi $ и $y=\rho \cdot \sin \phi $. Согласуем обозначения, приняв $u=\rho $, $v=\phi. $ Таким образом, $x=\vartheta \left(\rho ,\phi \right)=\rho \cdot \cos \phi $, $y=\psi \left(\rho ,\phi \right)=\rho \cdot \sin \phi $. Кроме того, $f\left(x,y\right)=f\left(\rho \cdot \cos \phi ,\rho \cdot \sin \phi \right).$ Вычисляя якобиан, получаем: Таким образом, формула для ДИ в полярных координатах имеет вид:$\iint \limits _{D}f\left(x,y\right)\cdot dx\cdot dy =\iint \limits _{D^{*} }f\left(\rho \cdot \cos \phi ,\rho \cdot \sin \phi \right)\cdot \rho \cdot d\rho \cdot d\phi $. С целью вычисления ДИ в полярных координатах сводят к повторному. Предположим, что область $D^{*} $ в полярных координатах является правильной. Это означает, что она ограничена непрерывными кривыми $\rho =\rho _{1} \left(\phi \right)$ и $\rho =\rho _{2} \left(\phi \right)$, а также лучами $\phi =\alpha $ и $\phi =\beta $, причем $\rho _{1} \left(\phi \right)\le \rho _{2} \left(\phi \right)$ и $\alpha
Таким образом, имеем следующую формулу для вычисления ДИ в полярных координатах: Замена переменных в ДИ
Вычислить двойной интеграл $\iint \limits _{D}\left(x+y\right)\cdot dx\cdot dy $ по области $D$, ограниченной параболой $y=x^{2} $ и прямыми $y=x$, $x=2$ и $x=3$.
В нашей задаче область $D$ ограничена слева и справа вертикальными прямыми $x=2$ и $x=3$, снизу прямой $y=x$, а сверху -- параболой $y=x^{2} $. При этом она является правильной как в направлении оси $Ox$, так и в направлении оси $Oy$. В то же время нижняя и верхняя границы области $D$ представлены одним уравнением, а левая и правая границы содержат по два участка.
Поэтому вычисляем данный интеграл по формуле $\iint \limits _{D}f\left(x,y\right)\cdot dx\cdot dy =\int \limits _{a}^{b}dx\int \limits _{\vartheta _{1} \left(x\right)}^{\vartheta _{2} \left(x\right)}f\left(x,y\right)\cdot dy $. Применительно к условиям нашей задачи получаем:
\[\iint \limits _{D}\left(x+y\right)\cdot dx\cdot dy =\int \limits _{2}^{3}dx\int \limits _{x}^{x^{2} }\left(x+y\right)\cdot dy =\] \[=\int \limits _{2}^{3}\left[x\cdot y+\frac{y^{2} }{2} \right]_{x}^{x^{2} } \cdot dx =\int \limits _{2}^{3}\left(x^{3} +\frac{x^{4} }{2} -x^{2} -\frac{x^{2} }{2} \right)\cdot dx =\] \[=\int \limits _{2}^{3}\left(\frac{x^{4} }{2} +x^{3} -\frac{3}{2} \cdot x^{2} \right)\cdot dx =\left[\frac{x^{5} }{10} +\frac{x^{4} }{4} -\frac{x^{3} }{2} \right]_{2}^{3} =\] \[=\left(\frac{3^{5} }{10} +\frac{3^{4} }{4} -\frac{3^{3} }{2} \right)-\left(\frac{2^{5} }{10} +\frac{2^{4} }{4} -\frac{2^{3} }{2} \right)=27,85.\]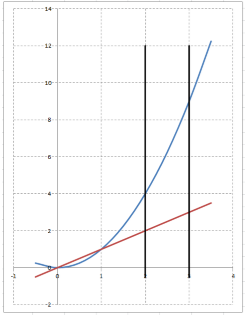
двойного интеграла">
