Длина радиус-вектора, который изображает заданное комплексное число $z=a+bi$, называется модулем данного комплексного числа.
Модуль заданного комплексного числа вычисляется по следующей формуле:
Вычислить модуль заданных комплексных чисел $z_{1} =13,\, \, z_{2} =4i,\, \, \, z_{3} =4+3i$.
Решение:
Модуль комплексного числа $z=a+bi$ вычислим по формуле: $r=\sqrt{a^{2} +b^{2} } $.
Для исходного комплексного числа $z_{1} =13$ получим $r_{1} =|z_{1} |=|13+0i|=\sqrt{13^{2} +0^{2} } =\sqrt{169} =13$
Для исходного комплексного числа $\, z_{2} =4i$ получим $r_{2} =|z_{2} |=|0+4i|=\sqrt{0^{2} +4^{2} } =\sqrt{16} =4$
Для исходного комплексного числа $\, z_{3} =4+3i$ получим $r_{3} =|z_{3} |=|4+3i|=\sqrt{4^{2} +3^{2} } =\sqrt{16+9} =\sqrt{25} =5$
Угол $\varphi $, образованный положительным направлением вещественной оси и радиус-вектором $\overrightarrow{OM} $, который соответствует заданному комплексному числу $z=a+bi$, называется аргументом данного числа и обозначается $\arg z$.
Модуль и аргумент заданного комплексного числа в явном виде используются при представлении комплексного числа в тригонометрической или показательной форме:
- $z=r\cdot (\cos \varphi +i\sin \varphi )$ - тригонометрическая форма;
- $z=r\cdot e^{i\varphi } $ - показательная форма.
Записать комплексное число в тригонометрической и показательной формах, заданное следующими данными: 1) $r=3;\varphi =\pi $; 2) $r=13;\varphi =\frac{3\pi }{4} $.
Решение:
1) Подставим данные $r=3;\varphi =\pi $ в соответствующие формулы и получим:
$z=3\cdot (\cos \pi +i\sin \pi )$ - тригонометрическая форма
$z=3\cdot e^{i\pi } $ - показательная форма.
2) Подставим данные $r=13;\varphi =\frac{3\pi }{4} $ в соответствующие формулы и получим:
$z=13\cdot (\cos \frac{3\pi }{4} +i\sin \frac{3\pi }{4} )$ - тригонометрическая форма
$z=13\cdot e^{i\frac{3\pi }{4} } $ - показательная форма.
Определить модуль и аргумент заданных комплексных чисел:
1) $z=\sqrt{2} \cdot (\cos 2\pi +i\sin 2\pi )$; 2) $z=\frac{5}{3} \cdot (\cos \frac{2\pi }{3} +i\sin \frac{2\pi }{3} )$; 3) $z=\sqrt{13} \cdot e^{i\frac{3\pi }{4} } $; 4) $z=13\cdot e^{i\pi } $.
Решение:
Модуль и аргумент найдем, используя формулы записи заданного комплексного числа в тригонометрической и показательной формах соответственно
1) Для исходного комплексного числа $z=\sqrt{2} \cdot (\cos 2\pi +i\sin 2\pi )$ получим $r=\sqrt{2} ;\varphi =2\pi $.
2) Для исходного комплексного числа $z=\frac{5}{3} \cdot (\cos \frac{2\pi }{3} +i\sin \frac{2\pi }{3} )$ получим $r=\frac{5}{3} ;\varphi =\frac{2\pi }{3} $.
3) Для исходного комплексного числа $z=\sqrt{13} \cdot e^{i\frac{3\pi }{4} } $ получим $r=\sqrt{13} ;\varphi =\frac{3\pi }{4} $.
4) Для исходного комплексного числа $z=13\cdot e^{i\pi } $ получим $r=13;\varphi =\pi $.
Аргумент $\varphi $ заданного комплексного числа $z=a+bi$ можно вычислить, используя следующие формулы:
На практике для вычисления значения аргумента заданного комплексного числа $z=a+bi$ обычно пользуются формулой:
$\varphi =\arg z=\left\{\begin{array}{c} {arctg\frac{b}{a} ,a\ge 0} \\ {arctg\frac{b}{a} +\pi ,a
или решают систему уравнений
$\left\{\begin{array}{c} {\cos \varphi =\frac{a}{\sqrt{a^{2} +b^{2} } } } \\ {\sin \varphi =\frac{b}{\sqrt{a^{2} +b^{2} } } } \end{array}\right. $. (**)
Вычислить аргумент заданных комплексных чисел: 1) $z=3$; 2) $z=4i$; 3) $z=1+i$; 4) $z=-5$; 5) $z=-2i$.
Решение:
1) $z=3$
Так как $z=3$, то $a=3,b=0$. Вычислим аргумент исходного комплексного числа, используя формулу (*):
2) $z=4i$
Так как $z=4i$, то $a=0,b=4$. Вычислим аргумент исходного комплексного числа, используя формулу (*):
3) $z=1+i$.
Так как $z=1+i$, то $a=1,b=1$. Вычислим аргумент исходного комплексного числа, решая систему (**):
Из курса тригонометрии известно, что $\cos \varphi =\sin \varphi =\frac{\sqrt{2} }{2} $ для угла, соответствующего первой координатной четверти и равного $\varphi =\frac{\pi }{4} $.
4) $z=-5$
Так как $z=-5$, то $a=-5,b=0$. Вычислим аргумент исходного комплексного числа, используя формулу (*):
5) $z=-2i$
Так как $z=-2i$, то $a=0,b=-2$. Вычислим аргумент исходного комплексного числа, используя формулу (*):
Аргумент вещественных чисел равен соответственно:
- 0 для положительного числа;
- $\pi $ для отрицательного числа.
Аргумент чисто мнимых чисел равен соответственно:
- $\frac{\pi }{2} $ с положительной мнимой частью;
- $\frac{3\pi }{2} $ с отрицательной мнимой частью.
Определить модуль и аргумент комплексных чисел, изображенных на комплексной плоскости (рис.)
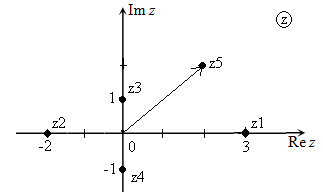
Решение:
Число $z_{1} $ изображено точкой $(3;0)$, следовательно, длина радиус-вектора равна 3, т.е. $r=3$, а аргумент $\varphi =0$ по примечанию 2.
Число $z_{2} $ изображено точкой $(-2;0)$, следовательно, длина соответствующего радиус-вектора равна 2, т.е. $r=2$, а аргумент $\varphi =\pi $ по примечанию 2.
Число $z_{3} $ изображено точкой $(0;1)$, следовательно, длина соответствующего радиус-вектора равна 1, т.е. $r=1$, а аргумент $\varphi =\frac{\pi }{2} $ по примечанию 3.
Число $z_{4} $ изображено точкой $(0;-1)$, следовательно, длина соответствующего радиус-вектора равна 1, т.е. $r=1$, а аргумент $\varphi =\frac{3\pi }{2} $ по примечанию 3.
Число $z_{5} $ изображено точкой $(2;2)$, следовательно, длина соответствующего радиус-вектора равна $\sqrt{2^{2} +2^{2} } =\sqrt{4+4} =\sqrt{8} =2\sqrt{2} $, т.е. $r=2\sqrt{2} $, а аргумент $\varphi =\frac{\pi }{4} $ по свойству прямоугольного треугольника.












