Рассмотрим решение уравнений с комплексными корнями и коэффициентами.
Двучленным называется уравнение вида $x^{n} =A$.
Рассмотрим три случая:
- В случае если $A$ - это положительное действительное число, то корни уравнения находятся по формуле
- В случае если $A$ - это отрицательное действительное число, то корни уравнения находятся по формуле
- В случае если $A$ - это комплексное число, то корни уравнения находятся по формуле
Решить уравнение: $x^{3} =8$.
Решение:
Так как $A>0$, то $x_{k} =\sqrt[{3}]{8} \cdot \left(\cos \frac{2k\pi }{3} +i\cdot \sin \frac{2k\pi }{3} \right),\, \, \, k=0,..,2$.
При $k=0$ получаем $x_{0} =\sqrt[{3}]{8} \cdot \left(\cos 0+i\cdot \sin 0\right)=\sqrt[{3}]{8} =2$.
При $k=1$ получаем
При $k=2$ получаем
Решить уравнение: $x^{3} =1+i$.
Решение:
Так как $A$ - комплексное число, то
Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(\cos \varphi +i\cdot \sin \varphi )$.
По условию $a=1,b=1$.
Вычислим модуль исходного комплексного числа:
Вычислим аргумент исходного комплексного числа:
Подставим полученные значения и получим:
Уравнение перепишем в виде:
При $k=0$ получаем $x_{0} =\sqrt[{3}]{\sqrt{2} } \cdot \left(\cos \frac{\pi /4}{3} +i\cdot \sin \frac{\pi /4}{3} \right)=\sqrt[{3}]{\sqrt{2} } \cdot \left(\cos \frac{\pi }{12} +i\cdot \sin \frac{\pi }{12} \right)=\sqrt[{6}]{2} \cdot \left(\cos \frac{\pi }{12} +i\cdot \sin \frac{\pi }{12} \right)$.
При $k=1$ получаем
При $k=2$ получаем
Квадратным называется уравнение вида $ax^{2} +bx+c=0$, где коэффициенты $a,b,c$ в общем случае являются некоторыми комплексными числами.
Решение квадратного уравнения находится с помощью дискриминанта $D=b^{2} -4ac$, при этом
В случае, когда дискриминант является отрицательным числом, корни данного уравнения являются комплексными числами.
Решить уравнение $x^{2} +2x+5=0$ и изобразить корни на плоскости.
Решение:
Вычислим дискриминант:
Так как $D
Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 1.
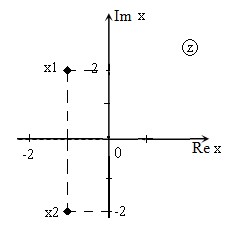
Рис. 1
В случае, когда уравнение имеет комплексные корни, они являются комплексно-сопряженными числами.
Комплексное число вида $\overline{z}=a-bi$ называется числом комплексно-сопряженным для $z=a+bi$.
Известно, что если $x_{1,2} $ являются корнями квадратного уравнения $ax^{2} +bx+c=0$, то данное уравнение можно переписать в виде $(x-x_{1} )(x-x_{2} )=0$. В общем случае $x_{1,2} $ являются комплексными корнями.
Зная корни уравнения $x_{1,2} =1\pm 2i$, записать исходное уравнение.
Решение:
Запишем уравнение следующим образом:
Выполним умножение комплексных чисел
Следовательно, $x^{2} -2x+5=0$ - искомое уравнение.
Рассмотрим квадратное уравнение с комплексными коэффициентами.
Решить уравнение: $z^{2} +(1-2i)\cdot z-(1+i)=0$ и изобразить корни на плоскости.
Решение:
Вычислим дискриминант:
Так как $D>0$, уравнение имеет два корня:
Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 2.
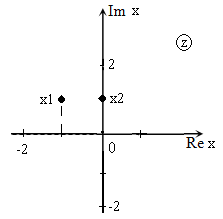
Рис. 2
В случае, когда уравнение имеет комплексные коэффициенты, его корни не обязательно являются комплексно-сопряженными числами.












