После долгих сомнений, которые длились более столетия, известные математики пришли к единому заключению, что необходимо ввести некоторый новый вид чисел, который назвали комплексными числами.
Выражение вида $z=a+bi$, где $a$ и $b$ - вещественные числа, а $i$ - «мнимая единица», называется комплексным числом $z$. Мнимая единица определяется равенством $i=\sqrt{-1} $ или $i^{2} =-1$.
Комплексное число вида $\overline{z}=a-bi$ называется числом комплексно-сопряженным для $z=a+bi$.
Записать комплексно-сопряженные числа для заданных комплексных чисел:
$1) z_{1} =12+3i; 2) z_{2} =5; 3) z_{3} =-2i.$
Решение:
Для комплексного числа $z=a+bi$ комплексно-сопряженным будет являться число $\overline{z}=a-bi$.
Для числа $z_{1} =12+3i$ получим $\overline{z_{1} }=12-3i$.
Для числа $z_{2} =5$ получим $\overline{z_{2} }=5$.
Для числа $z_{3} =-2i$ получим $\overline{z_{3} }=2i$.
Некоторые комплексные числа $z_{1} =a_{1} +b_{1} i$ и $z_{2} =a_{2} +b_{2} i$ называются равными, если выполняются следующие равенства $a_{1} =a_{2} ,b_{1} =b_{2} $. Обозначение: $z_{1} =z_{2} $.
Любое комплексное число можно изобразить на плоскости, которую принято называть комплексной плоскостью. Комплексная плоскость аналогична прямоугольной декартовой системе координат, исключение составляют только названия осей:
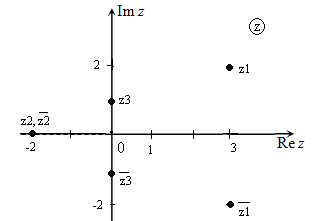
Рис. 1
Выделяют три формы представления (записи) комплексных чисел:
- алгебраическая;
- тригонометрическая;
- показательная.
Алгебраическая форма записи
Запись некоторого комплексного числа $z$ в виде $z=a+bi$ называется алгебраической формой записи (или алгебраической записью) комплексного числа. При этом:
$a$ - вещественная (действительная) часть, обозначение $Rez=a$;
$b$ - мнимая часть, обозначение $Imz=b$.
Тригонометрическая форма записи
Запись комплексного числа $z$ в виде $z=r\cdot (\cos \varphi +i\sin \varphi )$ называется тригонометрической формой записи, где число $r$ - модуль комплексного числа $z$, определяемый формулой $r=|z|=|a+bi|=\sqrt{a^{2} +b^{2} } $, а $\varphi $ - аргумент комплексного числа $z$, определяемый по формуле $\varphi =arctg\frac{b}{a} $.
Показательная форма записи
Запись комплексного числа $z$ в виде $z=r\cdot e^{i\varphi } $ называется показательной формой записи, где число $r$ - модуль комплексного числа $z$, определяемый по формуле $r=|z|=|a+bi|=\sqrt{a^{2} +b^{2} } $, $\varphi $ - аргумент комплексного числа $z$, определяемый по формуле $\varphi =arctg\frac{b}{a} $.
Над комплексными числами можно выполнять следующие действия: сложение, вычитание, умножение, деление, возведение в степень, извлечение корня.
Операции над комплексными числами
Сумма
Суммой двух заданных комплексных чисел $z_{1} =a_{1} +b_{1} i$ и $z_{2} =a_{2} +b_{2} i$ является комплексное число, которое определяется равенством $z_{1} +z_{2} =(a_{1} +b_{1} i)+(a_{2} +b_{2} i)=(a_{1} +a_{2} )+(b_{1} +b_{2} )\cdot i. $
Разность
Разностью двух заданных комплексных чисел $z_{1} =a_{1} +b_{1} i$ и $z_{2} =a_{2} +b_{2} i$ является комплексное число, которое определяется равенством $z_{1} -z_{2} =(a_{1} +b_{1} i)-(a_{2} +b_{2} i)=(a_{1} -a_{2} )+(b_{1} -b_{2} )\cdot i.$
Произведение
Произведением двух заданных комплексных чисел $z_{1} =a_{1} +b_{1} i$ и $z_{2} =a_{2} +b_{2} i$ является комплексное число, которое получается перемножением данных чисел по правилам алгебры с учетом того, что $i^{2} =-1$.
Произведением двух заданных комплексных чисел $z_{1} =r_{1} \cdot (\cos \varphi _{1} +i\sin \varphi _{1} )$ и $z_{2} =r_{2} \cdot (\cos \varphi _{2} +i\sin \varphi _{2} )$ является комплексное число, которое определяется равенством $z_{1} \cdot z_{2} =r_{1} \cdot r_{2} \cdot [\cos (\varphi _{1} +\varphi _{2} )+i\sin (\varphi _{1} +\varphi _{2} )].$
Частное
Частным двух заданных комплексных чисел $z_{1} =r_{1} \cdot (\cos \varphi _{1} +i\sin \varphi _{1} )$ и $z_{2} =r_{2} \cdot (\cos \varphi _{2} +i\sin \varphi _{2} )$ является комплексное число, которое определяется равенством $z_{1} \cdot z_{2} =\frac{r_{1} }{r_{2} } \cdot [\cos (\varphi _{1} -\varphi _{2} )+i\sin (\varphi _{1} -\varphi _{2} )].$
Степень порядка
Степенью порядка $n$ комплексного числа $z=r\cdot (\cos \varphi +i\sin \varphi )$ является комплексное число, которое определяется равенством $z^{n} =r^{n} \cdot (\cos n\varphi +i\sin n\varphi _{1} ). $
Данная формула называется формулой Муавра.
Корень
Корнем $n$-й степени комплексного числа $z=r\cdot (\cos \varphi +i\sin \varphi )$ является комплексное число, которое определяется равенством $\sqrt[{n}]{z} =\sqrt[{n}]{r} \cdot (\cos \frac{\varphi +2\pi k}{n} +i\sin \frac{\varphi +2\pi k}{n} ),\, \, \, k=0..n-1.$
Выполнить действия: 1) $z_{1} +z_{2} $; 2) $z_{1} -z_{2} $; 3) $z_{1} \cdot z_{2} $ для комплексных чисел $z_{1} =1+3i$ и $z_{2} =1-2i$.
Решение:
$1) z_{1} +z_{2} =(1+3i)+(1-2i)=(1+1)+(3-2)i=2+i $
$2) z_{1} +z_{2} =(1+3i)-(1-2i)=(1-1)-(3+2)i=0-5i=-5i $
$3) z_{1} \cdot z_{2} =(1+3i)\cdot (1-2i)=1\cdot 1+1\cdot 3i-1\cdot 2i-3\cdot 2\cdot i^{2} =1+3i-2i+6=7+i $
Выполнить умножение и деление заданных комплексных чисел:
$z_{1} =\sqrt{3} \cdot (\cos \pi +i\cdot \sin \pi )$ и $z_{2} =\sqrt{3} \cdot (\cos \pi +i\cdot \sin \pi )$.
Решение:
1) ${z_{1} \cdot z_{2} =\left(\sqrt{3} \cdot (\cos \pi +i\cdot \sin \pi )\right)\cdot \left(\sqrt{3} \cdot (\cos \pi +i\cdot \sin \pi )\right)=\sqrt{3} \cdot \sqrt{3} \cdot [\cos (\pi +\pi )+i\cdot \sin (\pi +\pi )]=} \\ {=3\cdot (\cos 2\pi +i\cdot \sin 2\pi )}$
2) ${z_{2} =\left(\sqrt{3} \cdot (\cos \pi +i\cdot \sin \pi )\right)\div \left(\sqrt{3} \cdot (\cos \pi +i\cdot \sin \pi )\right)=\frac{\sqrt{3} }{\sqrt{3} } \cdot [\cos (\pi -\pi )+i\cdot \sin (\pi -\pi )]=} \\ {=1\cdot (\cos 0+i\cdot \sin 0)=\cos 0+i\cdot \sin 0}$
Многочлен
Многочленом $n$-ой степени называется функция
$P_{n} (z)=a_{n} z^{n} +a_{n-1} z^{n-1} +a_{n-2} z^{n-2} +...+a_{1} z+a_{0} , $
где коэффициенты $a_{0} ,a_{1} ,a_{2} ,...,a_{n-1} ,a_{n} $ -- постоянные комплексные числа, $a_{n} \ne 0$, $z\in Z$ -- комплексная переменная. Число $z_{0} $, при котором заданный многочлен принимает нулевое значение ($P_{n} (z_{0} )=0$), называется корнем этого многочлена.
Любой многочлен степени $n$ может быть представлен как разложение многочлена на $n$ линейных сомножителей вида $z-a$ и множитель, который равен коэффициенту при $z^{n} $:
$$P_{n} (z)=A_{0} \cdot (z-a_{1} )\cdot (z-a_{2} )\cdot ...\cdot (z-a_{n} ), $$где $a_{1} ,a_{2} ,...,a_{n} $ -- корни многочлена.
Если в разложении многочлена степени $n$ на линейные множители
$P_{n} (x)=A_{0} \cdot (z-a_{1} )\cdot (z-a_{2} )\cdot ...\cdot (z-a_{n} ), (*) $некоторые линейные сомножители оказываются одинаковыми, то данные множители можно объединить, тогда разложение заданного многочлена на сомножители будет иметь следующий вид:
$$P_{n} (z)=A_{0} \cdot (z-a_{1} )^{k_{1} } \cdot (z-a_{2} )^{k_{2} } \cdot ...\cdot (z-a_{n} )^{k_{m} } (k_{1} +k_{2} +...+k_{m} =n). $$В формуле (*) корни многочлена $a_{1} ,a_{2} ,...,a_{n} $ могут быть не только вещественными, но и комплексными числами.
Для многочленов определены следующие операции: вычитание, сложение, умножение. Операция деления многочленов определена не для любых двух многочленов, однако, как и для целых чисел, имеется возможность выполнить деление с остатком.












