Предварительные сведения
Для начала разберемся с таким понятием, как четырехугольник.
Четырехугольником называется многоугольник, у которого $4$ вершины.
Четырехугольник имеет $4$ стороны, $4$ вершины и $4$ угла. Стороны, не имеющие общих вершин, называют противоположными сторона четырехугольника, в противном случае они называются смежными. Углы, не имеющие общих сторон, также называют смежными.
Рассмотрим далее подробно параллелограмм и трапецию.
Параллелограмм
Параллелограмм -- это четырехугольник, в котором противоположные стороны параллельны между собой (рис. 1).
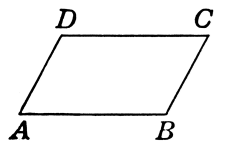
Рисунок 1. Параллелограмм
Параллелограмм имеет два основных свойства. Введем и докажем их.
Свойство 1: Противоположные стороны и углы параллелограмма равны, соответственно, между собой.
Доказательство.
Пусть нам дан параллелограмм $ABCD$. Проведем в нем диагональ $AC$ (рис. 2).
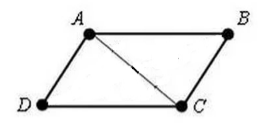
Рисунок 2.
Рассмотрим параллельные прямые $AB$ и $CD$ и их секущую $AC$. Тогда
как накрест лежащие углы.
Рассмотрим параллельные прямые $AD$ и $CB$ и их секущую $AC$. Тогда
как накрест лежащие углы.
Следовательно, $\angle A=\angle C$.
По $II$ признаку равенства треугольников,
так как $AC$ -- их общая сторона. Значит
Свойство доказано.
Свойство 2: Диагонали, проведенные в параллелограмме, делятся пополам их точкой пересечения.
Доказательство.
Пусть нам дан параллелограмм $ABCD$. Проведем в нем диагонали $AC$ и $BD$. Пусть они пересекаются в точке $O$ (рис. 3).
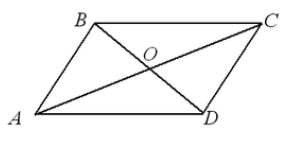
Рисунок 3.
Рассмотрим параллельные прямые $AB$ и $CD$ и их секущие $AC$ и $BD$. Тогда
как накрест лежащие углы.\textit{}
Так как, по свойству $1$, $AB=CD$, то, по II признаку равенства треугольников,
Следовательно,
Свойство доказано.
Трапеция
Трапеция -- это четырехугольник, в котором две противоположные стороны параллельны между собой, а другие две противоположные стороны не параллельны между собой (рис. 4).
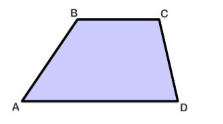
Рисунок 4. Трапеция
При этом параллельные стороны называют основаниями трапеции, а две другие -- боковыми сторонами трапеции.
Выделяют следующие виды трапеций.
[Определение] Если у трапеции не параллельные (боковые) стороны равны между собой, то её называют равнобедренной. [/Определение]
Если у трапеции два один угол прямой, то её называют равнобедренной.
В отличных от определений $4$ и $5$ случаях, трапецию называют разнобокой (рис. 5).
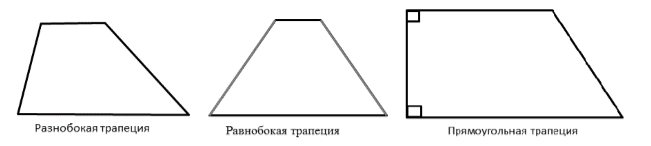
Рисунок 5. Виды трапеций
Трапеция обладает следующим свойством.
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство.
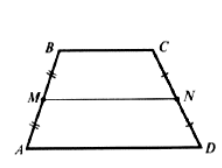
Пусть нам дана трапеция $ABCD$ с основаниями $AD\ и\ BC$. И пусть $MN$ -- средняя линия этой трапеции (рис. 6).
 Средняя линия трапеции">
Средняя линия трапеции">
Рисунок 6. Средняя линия трапеции
Докажем, что $MN||AD\ и\ MN=\frac{AD+BC}{2}$.
Рассмотрим вектор $\overrightarrow{MN}$. Используем далее правило многоугольника для сложения векторов. С одной стороны получим, что $\overrightarrow{MN}=\overrightarrow{MB}+\overrightarrow{BC}+\overrightarrow{CN}$
С другой стороны $\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AD}+\overrightarrow{DN}$
Сложим два последних равенства, получим
\[2\overrightarrow{MN}=\overrightarrow{MB}+\overrightarrow{BC}+\overrightarrow{CN}+\overrightarrow{MA}+\overrightarrow{AD}+\overrightarrow{DN}=\overrightarrow{BC}+\overrightarrow{AD}\]Следовательно
\[\overrightarrow{MN}=\frac{\overrightarrow{BC}+\overrightarrow{AD}}{2}\]Из этого же равенства (так как $\overrightarrow{BC}$ и $\overrightarrow{AD}$ сонаправлены, а, следовательно, коллинеарны) получаем, что $MN||AD$.
Теорема доказана.
Пример задачи
Боковые стороны трапеции равны $17\ см$ и $19\ см$ соответственно. Периметр трапеции равен $50\ см$. Найти длину средней линии трапеции.
Решение.
Сложим боковые стороны, получим $17\ см+19\ см=36\ см$
Значит, зная периметр равный $50\ см$, сумма оснований
\[50\ см-36\ см=14\ см\]Следовательно, по теореме $1$, средняя линия равна $\frac{14\ см}{2}=7\ см$












