Если закономерности изменений тех или иных физических величин каким-то образом связаны с понятием скорости, то в соответствующих математических зависимостях, кроме самих величин, появляются также и их производные различных порядков. Такие математические зависимости называют дифференциальными уравнениями.
Рассмотрим основные понятия, связанные с применением дифференциальных уравнений.
Например, экспериментально установлено, что скорость распада радиоактивного вещества в каждый момент времени пропорциональна его имеющейся массе. На основании этого физического факта можно определить закон изменения массы $m=m\left(t\right)$ радиоактивного вещества в зависимости от времени $t$.
Если в течение времени $\Delta t$ распалась масса $\Delta m$ радиоактивного вещества, то средняя скорость её распада равна $\frac{\Delta m}{\Delta t} $. Предел этого отношения при $\Delta t\to 0$ дает скорость распада вещества в момент $t$, то есть $\mathop{\lim }\limits_{\Delta t\to 0} \; \frac{\Delta m}{\Delta t} =\frac{dm}{dt} $. По условию задачи $\frac{dm}{dt} $ пропорциональна массе $m$, то есть $\frac{dm}{dt} =k\cdot m$, где $k$ -- коэффициент пропорциональности. Полученное уравнение можно также представить в виде $dm=k\cdot m\cdot dt$. Первое из этих уравнений содержит производную $\frac{dm}{dt} $, а второе -- дифференциал $dm$ искомой функции $m=m\left(t\right)$.
Что такое дифференциальное уравнение
Уравнение, связывающее независимую переменную, неизвестную функцию одной переменной, а также её производные или дифференциалы различных порядков, называется обыкновенным дифференциальным уравнением.
Обыкновенными дифференциальными уравнениями являются уравнения $2\cdot x\cdot y-y'=0$, $y'+8\cdot y''=1-\ln x$, $dy\cdot \left(x+5\cdot y\right)=dx\cdot \left(x-y\right)$, так как в них входят производные либо дифференциалы неизвестной функции одной переменной $y=y\left(x\right)$.
Кроме обыкновенных, существуют также дифференциальные уравнения в частных производных, в состав которых входят неизвестные функции, зависящие от двух и более переменных.
Порядком дифференциального уравнения называется порядок старшей производной, которая входит в это уравнение.
Уравнение $y'\cdot \sin x+y\cdot \cos y=1$ -- дифференциальное уравнение первого порядка, уравнение $\frac{d^{2} y}{dx^{2} } =\cos x+1$ -- дифференциальное уравнение второго порядка, $y'''=x^{2} +y$ -- дифференциальное уравнение третьего порядка и т. д.
Простейшими среди дифференциальных уравнений являются дифференциальные уравнения первого порядка. Для них используют различные формы записи:
- $y'=f\left(x,\; y\right)$ или $\frac{dy}{dx} =f\left(x,\; y\right)$ -- дифференциальное уравнение первого порядка, разрешенное относительно производной, например, $y'=x\cdot \sin \left(2\cdot y\right)$;
- $F\left(x,\; y,\; y'\right)=0$ -- дифференциальное уравнение первого порядка в неявной форме, например, $x\cdot y'+y\cdot \sin y'=0$;
- $P\left(x,\; y\right)\cdot dx+Q\left(x,\; y\right)\cdot dy=0$ -- дифференциальное уравнение первого порядка в симметричной форме, где $P\left(x,\; y\right)$ и $Q\left(x,\; y\right)$ -- заданные функции, например, $x^{3} \cdot dx+y^{3} \cdot dy=0$.
Таким образом, дифференциальное уравнение распада радиоактивного вещества $\frac{dm}{dt} =k\cdot m$ является обыкновенным дифференциальным уравнением первого порядка, разрешенным относительно производной.
Как решить дифференциальные уравнения
С целью решения перепишем это уравнение в виде $\frac{dm}{m} =k\cdot dt$. Замечаем, что $d\left(\ln m\right)=\frac{dm}{m} $ и $d\left(k\cdot t\right)=k\cdot dt$. Следовательно, $d\left(\ln m\right)=d\left(k\cdot t\right)$. Находим неопределенный интеграл от обоих частей этого равенства, используя то, что неопределенный интеграл от дифференциала некоторой функции равен самой этой функции плюс произвольная постоянная. Взяв произвольную постоянную в виде $\ln C$, получаем $\ln m=k\cdot t+\ln C$. Выполняем преобразования: $\ln m-\ln C=k\cdot t$; $\ln \frac{m}{C} =k\cdot t$; $\frac{m}{C} =e^{k\cdot t} $. Отсюда зависимость массы радиоактивного вещества от времени имеет вид $m=C\cdot e^{k\cdot t} $.
Таким образом, мы видим, что в отличие от алгебраических уравнений, решениями которых являются числа, решениями дифференциальных уравнений являются функции. Кроме того, полученная зависимость массы радиоактивного вещества от времени доказывает, что соответствующее дифференциальное уравнение имеет не единственное решение.
Общим решением обыкновенного дифференциального уравнения первого порядка называется функция $y=\phi \left(x,\; C\right)$, которая зависит от аргумента $x$, содержит произвольную постоянную $C$ и при подстановке её в уравнение превращает его в тождество.
Например, не сложно убедиться, что функция $m=C\cdot e^{k\cdot t} $ является общим решением дифференциального уравнения $\frac{dm}{m} =k\cdot dt$. Действительно, $dm=d\left(C\cdot e^{k\cdot t} \right)=C\cdot k\cdot e^{k\cdot t} \cdot dt$ или $dm=k\cdot m\cdot dt$, откуда $\frac{k\cdot m\cdot dt}{m} \equiv k\cdot dt$. Таким образом, общее решение представляет бесконечное множество функций, которые отличаются между собой конкретным значением произвольной постоянной~$C$. Эти функции являются представителями, так называемых, частных решений дифференциального уравнения.
Частным решением дифференциального уравнения называется функция $y=\phi \left(x,\; C_{0} \right)$, которую можно получить из общего решения при определенном значении произвольной постоянной $C=C_{0} $.
Например, функция $m=e^{k\cdot t} $ является частным решением дифференциального уравнения $\frac{dm}{m} =k\cdot dt$, полученным из общего решения $m=C\cdot e^{k\cdot t} $ при $C=1$.
Для получения из общего решения конкретного частного чаще всего используют начальное условие.
Условие $y\left(x_{0} \right)=y_{0} $, то есть при заданном $x=x_{0} $ значение функции $y$ должно равняться заданному числу $y_{0} $, которое накладывается на искомое решение $y=y\left(x\right)$ данного дифференциального уравнения, называется начальным условием.
Например, пусть для общего решения $m=C\cdot e^{k\cdot t} $ известно, что $m\left(0\right)=m_{0} $, то есть в начальный момент времени $t=0$ масса радиоактивного вещества $m$ была равна заданному числу $m_{0} $. Подставляем это начальное условие в общее решение и получаем $m_{0} =C\cdot e^{k\cdot 0} $, откуда $C=m_{0} $. Таким образом, благодаря начальному условию мы получили конкретное значение произвольной постоянной и конкретное частное решение $m=m_{0} \cdot e^{k\cdot t} $.
График частного решения обыкновенного дифференциального уравнения, построенный на плоскости $xOy$, называется интегральной кривой.
Таким образом, график функции $m=m_{0} \cdot e^{k\cdot t} $, которая представляет собой экспоненту, является интегральной кривой данного дифференциального уравнения $\frac{dm}{m} =k\cdot dt$.
Геометрически общее решение $m=C\cdot e^{k\cdot t} $ в целом представляет собой семейство интегральных кривых на плоскости $xOy$, зависящее от произвольной постоянной $C$. Например, на рисунке изображено семейство интегральных кривых, которое соответствует общему решению $m=C\cdot e^{-0,2\cdot t} $ дифференциального уравнения $\frac{dm}{m} =-0,2\cdot dt$.
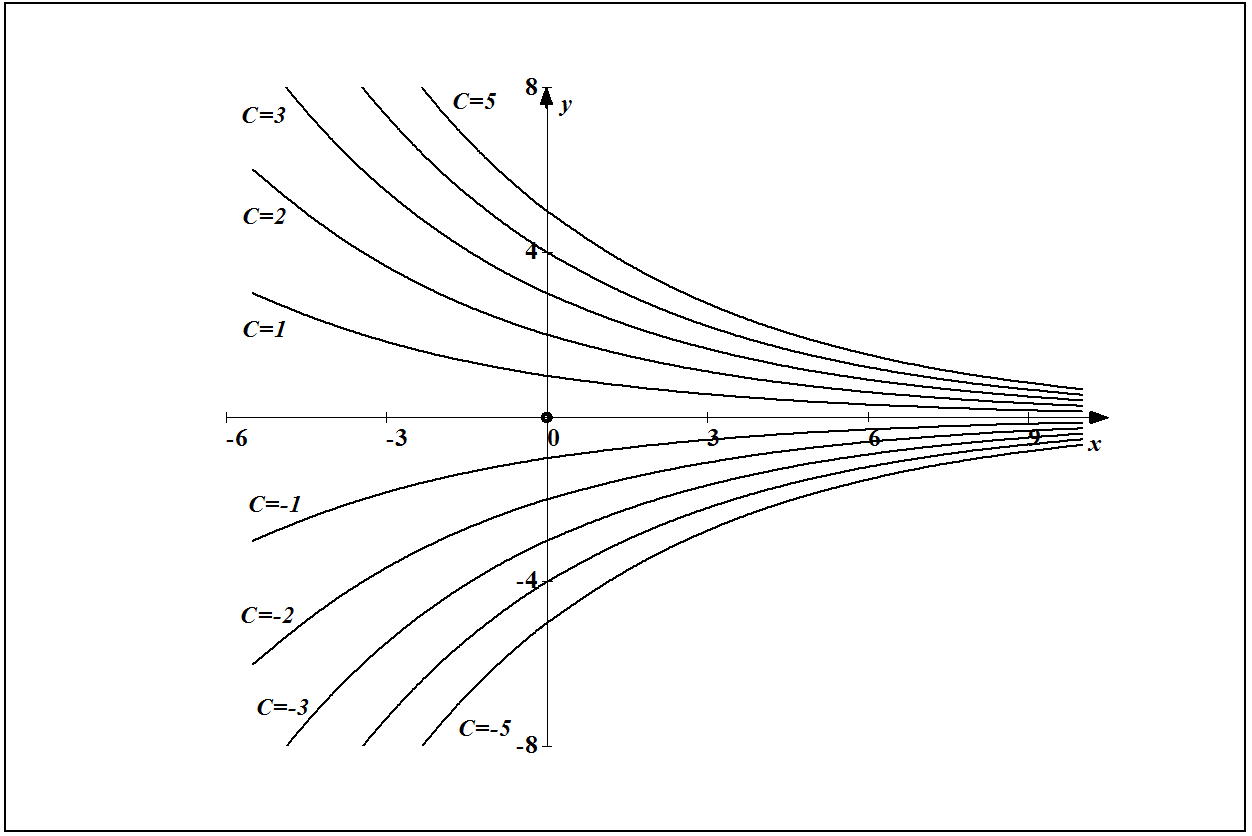
Начальное условие геометрически означает заданную точку $\left(x_{0} ,\; y_{0} \right)$, через которую должна проходить конкретная интегральная кривая из всего семейства интегральных кривых. Или, иначе говоря, частное решение, полученное из начального условия $y\left|_{x=x_{0} } \right. =y_{0} $, геометрически соответствует той единственной интегральной кривой из семейства, которая проходит через заданную точку $\left(x_{0} ,\; y_{0} \right)$.
Закон изменения массы $m=m_{0} \cdot e^{k\cdot t} $ радиоактивного вещества в зависимости от времени $t$ содержит неизвестный коэффициент пропорциональности $k$, значение которого можно найти из периода полураспада, то есть периода, в течение которого распадается половина имеющейся массы радиоактивного вещества.
Предположим, что радиоактивным веществом является радий, период полураспада которого составляет 1590 лет. Это дает возможность записать условие: $m=\frac{m_{0} }{2} $ при $t=1590$. Отсюда получаем: $\frac{m_{0} }{2} =m_{0} \cdot e^{k\cdot 1590} $, $\frac{1}{2} =e^{k\cdot 1590} $, $\frac{1}{2^{\frac{1}{1590} } } =e^{k} $ или $2^{-\frac{1}{1590} } =e^{k} $. Окончательно имеем: $m=m_{0} \cdot 2^{-\frac{t}{1590} } $. Эта формула дает закон распада радия.











