Образование полярной системы координат
На плоскости, кроме декартовой прямоугольной системы координат, используют также полярную систему координат. Это связано с тем, что сложность уравнений кривых зависит от системы координат, в которой они представляются. Поэтому при удачном выборе системы координат можно существенно упростить решение той или иной задачи.
Уравнение окружности радиуса $R$ с центром в начале координат в декартовой системе координат имеет вид: $x^{2} +y^{2} =R^{2} $. Уравнение той же окружности в полярной системе координат: $\rho =R$.
Полярная система координат вводится следующим образом. На плоскости вибираем некоторую точку $O$, которая называется полюсом. Из этой точки проводим луч $Ox$, который называется полярной осью. Выбираем линейный масштаб для измерения длин отрезков. Для измерения углов выбираем или градусную, или радианную меру.
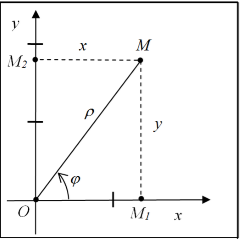
Положение точки $M$ на плоскости определяют два числа: число $\rho $ -- расстояние точки $M$ от полюса (полярный радиус $OM$), а также число $\phi $ -- угол, образованный полярным радиусом с полярной осью (полярный угол). Положительным направлением отсчета угла $\phi $ считается направление против часовой стрелки.
Числа $\rho $ и $\phi $ называются полярными координатами точки $M\left(\rho ,\; \phi \right)$. При этом полярный радиус $\rho \ge 0$, а полярный угол $0\le \phi
Связь между прямоугольными и полярными координатами
Между полярными и декартовыми прямоугольными координатами точки $M$ можно установить связь. Для этого нужно совместить полюс и полярную ось с началом и положительным направлением оси $Ox$ прямоугольной системы координат.
Из треугольника $OMM_{1} $ получаем следующие формулы связи:
- для заданных полярных координат $\rho $ и $\phi $ декартовы координаты $x$ и $y$ вычисляются по формулам $x=\rho \cdot \cos \phi $ и $y=\rho \cdot \sin \phi $;
- для заданных декартовых координат $x$ и $y$ полярные координаты $\rho $ и $\phi $ вычисляются по формулам $\rho =\sqrt{x^{2} +y^{2} } $ и $\phi =Arctg\frac{y}{x} $.
Обратная тригонометрическая функция $\phi =Arctg\frac{y}{x} $ многозначна, поэтому при практических вычислениях пользуются главным значением $ - \frac{\pi }{2}
Общая формула имеет вид:
\[\phi =\left\{\begin{array}{l} {arctg\frac{y}{x} \; \; при \; x>0,\; y>0} \\ {\pi +arctg\frac{y}{x} \; \; при \; x0,\; y0} \\ {\frac{3\cdot \pi }{2} \; при \; x=0,\; yПри $x=0$ и $y=0$ имеем $\rho =\sqrt{x^{2} +y^{2} } =0$. В этом случае значение угла $\phi $ можно взять произвольно.Некоторые важнейшие кривые
- Циссоида. Уравнения: $y^{2} =\frac{x^{3} }{a-x} $ -- в декартовых прямоугольных координатах; $\rho =\frac{a\cdot \sin ^{2} \phi }{\cos \phi } $ -- в полярных координатах.
- Строфоида. Уравнения: $y^{2} =x^{2} \cdot \frac{a+x}{a-x} $ -- в декартовых прямоугольных координатах; $\rho =-a\cdot \frac{\cos \left(2\cdot \phi \right)}{\cos \phi } $ -- в полярных координатах.
- Кардиоида. Уравнения: $\left(x^{2} +y^{2} \right)^{2} -2\cdot a\cdot x\cdot \left(x^{2} +y^{2} \right)=a^{2} \cdot y^{2} $ -- в декартовых прямоугольных координатах; $\rho =a\cdot \left(1+\cos \phi \right)$ -- в полярных координатах.
-
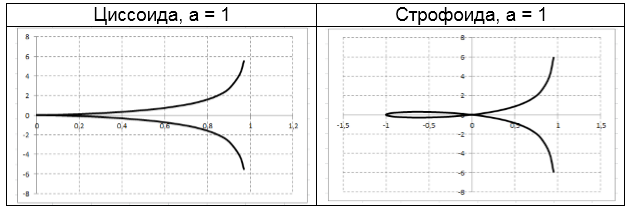
- Лемниската. Уравнения: $\left(x^{2} +y^{2} \right)^{2} -2\cdot a^{2} \cdot \left(x^{2} -y^{2} \right)=0$ -- в декартовых прямоугольных координатах; $\rho =a\cdot \sqrt{2\cdot \cos \left(2\cdot \phi \right)} $ -- в полярных координатах.
При построении графиков в полярных координатах с помощью средств MS Excel имеются некоторые особенности.
График в MS Excel может быть построен, если функция однозначна и задана в декартовой прямоугольной системе координат.
Для построения графика циссоиды $y^{2} =\frac{x^{3} }{a-x} $ следует использовать уравнения $y=+\sqrt{\frac{x^{3} }{a-x} } $ и $y=-\sqrt{\frac{x^{3} }{a-x} } $.
При построении графика строфоиды поступаем аналогично.
Для построения графиков кардиоиды и лемнискаты такой прием не подходит, так как разрешить их уравнения в декартовой прямоугольной системе координат относительно $y$ невозможно.
Поэтому рекомендуется использовать уравнения этих кривых в полярных координатах по следующей схеме: задать значение угла $\phi $ в градусах (так удобнее), перевести это значение в радианы, в соответствии с уравнением кривой вычислить значение $\rho $, вычислить декартовы координаты $x$ и $y$ по формулам $x=\rho \cdot \cos \phi $ и $y=\rho \cdot \sin \phi $. Теперь можно строить график обычным образом.












