Предварительные сведения
Для того чтобы мы могли ввести понятие смешанного произведения векторов, нужно сначала вспомнить понятия скалярного и векторного произведений этих векторов.
Скалярным произведением двух векторов будем называть такой скаляр (или число), который равняется произведению длин двух этих векторов с косинусом угла между данными векторами.
Математически это может выглядеть следующим образом:
$\overline{α}\overline{β}=|\overline{α}||\overline{β}|cos∠(\overline{α},\overline{β})$
Также, помимо того, как из самого определения 1, для нахождения скалярного произведения можно пользоваться следующей теоремой.
Скалярное произведение двух данных векторов $\overline{α}$ и $\overline{β}$ равняется сумме произведений их соответствующих координат.
Математически выглядит следующим образом
$\overline{α}\overline{β}=α_1 α_2+β_1 β_2$
Обозначение: $\overline{α}\cdot \overline{β}$.
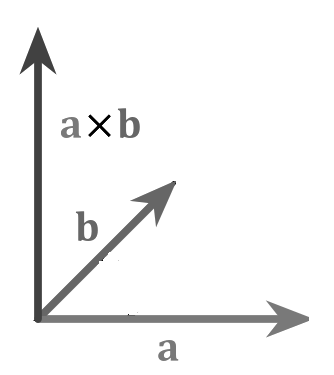
Векторным произведением двух векторов будем называть такой вектор, который будет перпендикулярен обоим данным векторам, и его длина будет равняться произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют туже ориентацию, как и декартова система координат.
Обозначение: $\overline{α}х\overline{β}$.
Математически это выглядит следующим образом:
- $|\overline{α}х\overline{β}|=|\overline{α}||\overline{β}|sin∠(\overline{α},\overline{β})$
- $\overline{α}х\overline{β}⊥\overline{α}$, $\overline{α}х\overline{β}⊥\overline{β}$
- $(\overline{α}х\overline{β},\overline{α},\overline{β})$ и $(\overline{i},\overline{j},\overline{k})$ одинаково ориентированы (рис. 1)
Понятие смешанного произведения векторов
Смешанным произведением векторов $\overline{α}$, $\overline{β}$ и $\overline{γ}$ будем называть такой скаляр (или число), которое будет равняться скалярному произведению первого вектора $\overline{α}$ на вектор векторного произведения $\overline{β}х\overline{γ}$ двух других векторов.
Обозначение: $(\overline{α},\overline{β},\overline{γ})$.
Математически это выглядит следующим образом:
$(\overline{α},\overline{β},\overline{γ})=\overline{α}\cdot (\overline{β}х\overline{γ})$
Очевидно, что смешанное произведение будет равняться нулю в двух случаях:
- Если длина одного или нескольких векторов равняется нулю.
- Если эти векторы будут являться компланарными.
Найти значение смешанного произведения векторов $\overline{α}$, $\overline{β}$ и $\overline{γ}$, которые имеют координаты $(0,0,5)$, $(0,4,0)$ и $(3,0,0)$, соответственно.
Решение.
Из определений 1, и 3 будем получать
$(\overline{α},\overline{β},\overline{γ})=\overline{α}\cdot (\overline{β}х\overline{γ})=|\overline{a}||\overline{β}х\overline{γ}|cos∠(\overline{α},\overline{β}х\overline{γ})$
Изобразим эти векторы в декартовом координатном пространстве (рис. 2):
Найдем вначале длину вектора векторного произведения векторов $\overline{β}$ и $\overline{γ}$
Видим, что эти векторы лежат на осях $Ox$ и $Oy$, соответственно. Следовательно, угол между ними будет равняться $90^0$. Найдем длины этих векторов:
$|\overline{β}|=\sqrt{0+16+0}=4$
$|\overline{γ}|=\sqrt{9+0+0}=3$
Тогда, по определению 2, получим
$|\overline{β}х\overline{γ}|=|\overline{α}||\overline{β}|sin90^\circ=4\cdot 3\cdot 1=12$
Из 3 части определения 2 очевидно, что вектор $\overline{β}х\overline{γ}$ принадлежит оси $Oz$ и направлен в туже сторону, что и сама ось, следовательно, угол между векторами $\overline{α}$ и $\overline{β}х\overline{γ}$ равняется $0^\circ$.
Длина вектора $\overline{α}$
$|\overline{α}|=\sqrt{0+0+25}=5$
Получим
$(\overline{α},\overline{β},\overline{γ})=|\overline{a}||\overline{β}х\overline{γ}|cos∠(\overline{α},\overline{β}х\overline{γ})=5\cdot 12\cdot cos0^\circ=60$
Ответ: $60$.
Вычисление смешанного произведения по координатам векторов
Из определения 1 сразу же вытекает и способ нахождения смешанного произведения для трех данных векторов. Но существует еще способ нахождения с помощью координат данных нам векторов.
Пусть нам даны векторы $\overline{α}$, $\overline{β}$ и $\overline{γ}$, которые будут иметь координаты $(α_1,α_2,α_3)$, $(β_1,β_2,β_3)$ и $(γ_1,γ_2,γ_3)$, соответственно. Тогда значение смешанного произведения можно найти по следующей формуле:
$(\overline{α},\overline{β},\overline{γ})=\begin{vmatrix}α_1&α_2&α_3\\β_1&β_2&β_3\\γ_1&γ_2&γ_3\end{vmatrix}$
Иначе, получим
$\overline{α}х\overline{β}=α_1 β_2 γ_3+α_3 β_1 γ_2+α_2 β_3 γ_1-α_3 β_2 γ_1-α_2 β_1 γ_3-α_1 β_3 γ_2$
Найти значение смешанного произведения векторов $\overline{α}$, $\overline{β}$ и $\overline{γ}$ с координатами $(1,1,0)$, $(0,3,3)$ и $(-1,2,6)$.
Решение.
Воспользуемся формулой, приведенной выше. Получим
$(\overline{α},\overline{β},\overline{γ})=\begin{vmatrix}1&1&0\\0&3&3\\-1&2&6\end{vmatrix}=18+(-3)+0-0-6-0=18-9=9$
Ответ: $9$.
Свойства смешанного произведения векторов
Для произвольных четырех векторов $\overline{α}, $\overline{β}$, $\overline{γ}$ и $\overline{δ}$, а также $r∈R$ справедливы следующие свойства: справедливы следующие свойства:
1) При перестановке местами знаков произведений в смешанном произведении можно менять между собой
$(\overline{α},\overline{δ},\overline{γ})=\overline{α}\cdot (\overline{δ}х\overline{γ})=(\overline{α}х\overline{δ})\cdot \overline{γ}$
2) Векторы в смешанном произведении можно менять только циклически
$(\overline{α},\overline{δ},\overline{γ})=(\overline{δ},\overline{γ},\overline{α})=(\overline{γ},\overline{α},\overline{δ})$
3) Перемещение только одного вектора на другое место меняет знак
$(\overline{α},\overline{δ},\overline{γ})=-(\overline{β},\overline{α},\overline{γ})=-(\overline{γ},\overline{δ},\overline{α})=-(\overline{α},\overline{γ},\overline{δ})$
4) Из формулы выше, очевидны следующие равенства:
$(r\overline{α},\overline{δ},\overline{γ})=r(\overline{α},\overline{δ},\overline{γ})$
$(\overline{α},r\overline{δ},\overline{γ})=r(\overline{α},\overline{δ},\overline{γ})$
$(overlie{α},\overline{δ},r\overline{γ})=r(\overline{α},\overline{δ},\overline{γ})$
5) Справедливы равенства:
$(\overline{α}+\overline{β},\overline{δ},\overline{γ})=(\overline{α},\overline{δ},\overline{γ})+(\overline{β},\overline{δ},\overline{γ})$
$(\overline{α},\overline{δ}+\overline{β},\overline{γ})=(\overline{α},\overline{δ},\overline{γ})+(\overline{α},\overline{β},\overline{γ})$
$(\overline{α},\overline{δ},\overline{γ}+\overline{β})=(\overline{α},\overline{δ},\overline{γ})+(\overline{α},\overline{δ},\overline{β})$
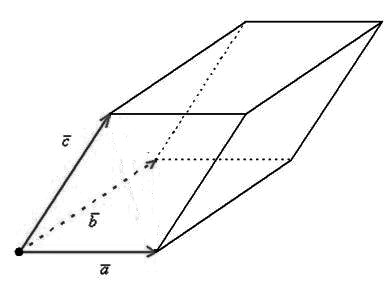
6) Геометрический смысл – площадь параллелепипеда (рис. 3):
$S=|(\overline{α},\overline{β},\overline{c})|$