Предварительные сведения
Вначале рассмотрим непосредственно понятие треугольника.
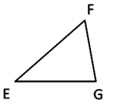
Треугольником будем называть геометрическую фигуру, которая составлена из трех точек, соединенных между собой отрезками (рис. 1).
Точки в рамках определения 1 будем называть вершинами треугольника.
Отрезки в рамках определения 1 будем называть сторонами треугольника.
Очевидно, что любой треугольник будет иметь 3 вершин, а также три стороны.
Соотношение сторон и углов в треугольнике
Введем следующую теорему.
В произвольном треугольнике напротив его большей стороны всегда лежит его больший угол.
Доказательство.
Пусть на рисунке 1 сторона $EF$ - большая сторона треугольника. Тогда нам нужно доказать, что угол $G$ будет большим углом в этом треугольнике.
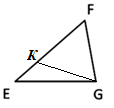
Отметим на большей стороне отрезок $FK=FG$ (рис. 2).
Так как $EF$ - большая сторона треугольника, то, очевидно, точка K будет лежать на этой стороне. Из этого следует, что
$∠G>∠KGF$
Угол $FKG$ будет внешним углом для треугольника $EKG$. Значит, по теореме о внешнем угле, имеем
$∠GKF=∠E+∠KGE$
Следовательно
$∠GKF>∠E$
Так как треугольник $GKF$ равнобедренный, то $∠GKF=∠KGF$
Из этого всего следует, что
$∠G>∠E$
Аналогично доказывается, что $∠G>∠F$.
Теорема доказана.
Эта теорема имеет обратную теорему. Сформулируем и докажем ее.
В произвольном треугольнике напротив его большего угла всегда лежит его большая сторона.
Доказательство.
Пусть на рисунке 1 угол $G$ больший угол треугольника. Тогда нам нужно доказать, что сторона $EF$ - большая сторона в этом треугольнике.
Предположим противное, что сторона $EF$ не является большей стороной. Тогда возможны следующие два случая развития событий.
-
Сторона $EF$ равняется стороне $FG$.
В этом случае треугольник $EFG$ будет равнобедренным и тогда $∠E=∠G$, что противоречит начальному условию теоремы.
-
Сторона $EF$ меньше стороны $FG$.
В этом случае, по теореме 1 будем иметь, что $∠G
Следовательно, сторона $EF$ – большая сторона в этом треугольнике.
Теорема доказана.
Из этих двух теорем можно вывести два следствия. Приведем их также в виде теорем и докажем.
Гипотенуза любого прямоугольного треугольника является большей стороной в этом треугольнике.
Доказательство.
Так как прямоугольный треугольник имеет один прямой и два острых угла, то прямой угол будет в нем большим. Тогда, по теореме 2, напротив прямого угла и будет находиться большая сторона. Она и будет, по определению прямоугольного треугольника, являться гипотенузой.
Теорема доказана.
Если в произвольном треугольнике будут два угла равны между собой, то такой треугольник будет равнобедренным.
Доказательство.
Из теорем 1 и 2 будет очевидно, что стороны напротив равных углов будут также равными. Следовательно, по определению равнобедренного треугольника, такой треугольник будет являться равнобедренным.
Теорема доказана.
Отметим, что последняя теорема также называется признаком равнобедренного треугольника.
Неравенство треугольника
Приведем и докажем теперь теорему, которую называют неравенством треугольника.
Сумма любых двух сторон в произвольном треугольника будет больше, чем его третья сторона.
Доказательство.
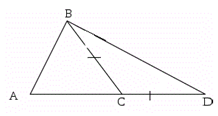
Рассмотрим произвольный треугольник $ABC$. Докажем, что
$BC+AC
В этом случае треугольник $BCD$ будет равнобедренным, значит, $∠CBD$ будет равняться $∠D$. Тогда, очевидно, что $∠ABD>∠D$. Следовательно, по теореме 2, $AD>AB$. Из равенства
$AD=AC+CD=AC+CB$
Получим, что
$AB
Теорема доказана.
Пример задачи
Сравнить стороны треугольника $ABC$, если $∠A
Решение.
Для решения используем теорему 2.
Получим, что
$BC