Понятие длины вектора
Для того, чтобы разобраться с понятием длины вектора, прежде всего надо разобрать само понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок. Введем следующее определение.
Отрезком будем называть часть прямой, которая имеет две границы в виде точек.
Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу - его концом. Направление указывается от его начала к концу отрезка.
Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.
Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).
Одной маленькой буквой: $\overline{a}$ (рис. 1).
Введем теперь, непосредственно, понятие длин вектора.
Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.
Обозначение: $|\overline{a}|$
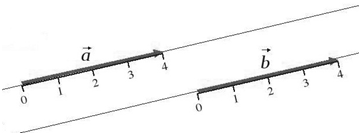
Понятие длины вектора связано, к примеру, с таким понятием, как равенство двух векторов.
Два вектора будем называть равными, если они удовлетворяют двух условиям: 1. Они сонаправлены; 1. Их длины равны (рис. 2).
Для того, чтобы определять векторы вводят систему координат и определяют координаты для вектора во введенной системе. Как мы знаем, любой вектор можно разложить в виде $\overline{c}=m\overline{i}+n\overline{j}$, где $m$ и $n$ – действительные числа, а $\overline{i}$ и $\overline{j}$ - единичные векторы на оси $Ox$ и $Oy$, соответственно.
Коэффициенты разложения вектора $\overline{c}=m\overline{i}+n\overline{j}$ будем называть координатами этого вектора во введенной системе координат. Математически:
$\overline{c}={m,n}$
Как найти длину вектора?
Для того, чтобы вывести формулу для вычисления длины произвольного вектора по данным его координатам рассмотрим следующую задачу:
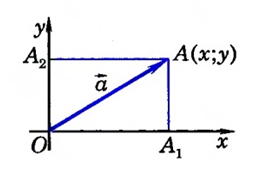
Дано: вектор $\overline{α}$, имеющий координаты ${x,y}$. Найти: длину этого вектора.
Решение.
Введем на плоскости декартову систему координат $xOy$. От начал введенной системы координат отложим $\overline{OA}=\overline{a}$. Построим проекции $OA_1$ и $OA_2$ построенного вектора на оси $Ox$ и $Oy$, соответственно (рис. 3).
Построенный нами вектор $\overline{OA}$ будет радиус вектором для точки $A$, следовательно, она будет иметь координаты ${x,y}$, значит
$[OA_1 ]=x$, $[ OA_2]=y$
Теперь мы легко можем найти искомую длину с помощью теоремы Пифагора, получим
$|\overline{α}|^2=[OA_1]^2+[OA_2]^2$
$|\overline{α}|^2=x^2+y^2$
$|\overline{α}|=\sqrt{x^2+y^2}$
Ответ: $\sqrt{x^2+y^2}$.
Вывод: Чтобы найти длину вектора, у которого задан его координаты, необходимо найти корень из квадрата суммы этих координат.
Пример задач
Найдите расстояние между точками $X$ и $Y$, которые имеют следующие координаты: $(-1,5)$ и $(7,3)$, соответственно.
Решение.
Любые две точки можно легко связать с понятием вектора. Рассмотрим, к примеру, вектор $\overline{XY}$. Как мы уже знаем, координаты такого вектора можно найти, вычтя из координат конечной точки ($Y$) соответствующие координаты начальной точки ($X$). Получим, что
$\overline{XY}=(7+1,3-5)=(8,-2)$
Теперь, найдя длину этого вектора по формуле, выведенной выше, мы и получим искомую длину. Получим:
$d=\sqrt{8^2+(-2)^2}=\sqrt{64+4}=\sqrt{68}=2\sqrt{17}$
Ответ: $2\sqrt{17}$.
Из этой задачи можно вывести формулу для вычисления такого расстояния. Пусть две точки имеют координаты ${(x',y')}$ и ${(x'',y'')}$. Тогда длину между такими точками можно найти по следующей формуле:
$d=\sqrt{(x'-x'')^2+(y'-y'')^2}$
Пусть нам дан треугольник своими координатами вершин $(5,-9)$, $(12,-2)$ и $(4,0)$. Найдем его периметр.
Решение.
Найдем для начала длины всех его сторон по формуле из замечания к задаче 2.
Первая сторона равняется:
$\sqrt{(5-12)^2+(-9+2)^2}=\sqrt{(-7)^2+(-7)^2}=\sqrt{98}=7\sqrt{2}$
Вторая сторона равняется:
$\sqrt{(5-4)^2+(-9-0)^2}=\sqrt{1^2+(-9)^2}=\sqrt{82}$
Третья сторона равняется:
$\sqrt{(12-4)^2+(-2-0)^2}=\sqrt{8^2+(-2)^2 }=\sqrt{68}=2\sqrt{17}$
Складывая, получим
Ответ: $7\sqrt{2}+\sqrt{82}+2\sqrt{17}$