К простейшим задачам в координатах относятся следующие задачи:
-
Вычисление координат вектора по координатам его начала и конца.
-
Нахождение координат середины отрезка.
-
Вычисление длины вектора.
-
Вычисление расстояние между двумя точками.
Рассмотрим далее решение этих задач.
Вычисление координат вектора по координатам его начала и конца
Перед тем, как ввести данную задачу напомним понятие радиус вектора данной точки.
Пусть точка $M$ дана в заданной системе координат с началом в точке $O$. Тогда вектор $\overrightarrow{OM}$ называется радиус-вектором для точки $M$.
Напомним, что при этом, если $M=\{x,y\}$ в данной системе координат, то вектор $\overrightarrow{OM}=\{x,y\}$ в этой системе координат.
Даны точки $A$ и $B$ имеющие координаты $\left\{x_1,\ y_1\right\}$ и $\{x_2,\ y_2\}$ соответственно. Найти координаты вектора $\overrightarrow{AB}.$
Решение.
Рассмотрим рисунок по данной задаче (Рис. 1).
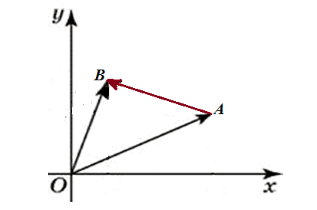
Рисунок 1. Связь между координатами вектора и координатами его начала и конца
По определению разности двух векторов, имеем
\[\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}\]Следовательно,
\[\overrightarrow{AB}=\left\{x_2,\ y_2\right\}-\left\{x_1,\ y_1\right\}=\{x_2-x_1,\ y_2-y_1\}\]Ответ: $\overrightarrow{AB}=\{x_2-x_1,\ y_2-y_1\}$.
Координаты середины отрезка
Даны точки $A$ и $B$ имеющие координаты $\left\{x_1,\ y_1\right\}$ и $\{x_2,\ y_2\}$ соответственно. $C$ -- середина отрезка $AB$. Найти координаты точки $C.$
Решение.
Обозначим координаты точки $C$ через $\left\{x,\ y\right\}$. Рассмотрим рисунок 2.
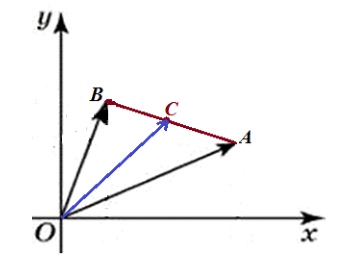
Рисунок 2. Середина отрезка
Из правила параллелограмма, получим
\[\overrightarrow{OC}=\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB})\]Так как векторы $\overrightarrow{OC},\ \overrightarrow{OA}\ и\ \overrightarrow{OB}$ - радиус-векторы точек $C,\ A\ и\ B$ соответственно, то получим
\[\overrightarrow{OC}=\left\{x,\ y\right\},\ \ \overrightarrow{OA}=\left\{x_1,\ y_1\right\},\ \ \overrightarrow{OB}=\{x_2,\ y_2\}\]Следовательно,
\[x=\frac{x_1+x_2}{2},\ y=\frac{y_1+y_2}{2}\]Ответ: $C=\left\{\frac{x_1+x_2}{2},\ \frac{y_1+y_2}{2}\right\}$
Вычисление длины вектора по его координатам
Дан вектор $\overrightarrow{a}$ с координатами $\left\{x,\ y\right\}$. Найти длину этого вектора.
Решение.
Рассмотрим систему координат $xOy$. Отложим от ее начала координат вектор $\overrightarrow{OA}=\overrightarrow{a}$. Проведем через точку $A$ перпендикуляры к осям координат $OA_1$ и $OA_2$ (рис. 3).
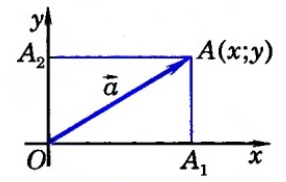
Рисунок 3. Вычисление длины вектора
Так как вектор $\overrightarrow{OA}$ - радиус вектор точки $A$, то $A=\left\{x,\ y\right\}$, следовательно,
\[OA_1=x,\ OA_2=y\]Найдем теперь длины вектора по теореме Пифагора:
\[{|\overrightarrow{a}|}^2={OA_1}^2+{OA_2}^2\] \[{|\overrightarrow{a}|}^2=x^2+y^2\] \[\left|\overrightarrow{a}\right|=\sqrt{x^2+y^2}\]Ответ: $\sqrt{x^2+y^2}$.
Расстояние между двумя точками
Даны точки $A$ и $B$ имеющие координаты $\left\{x_1,\ y_1\right\}$ и $\{x_2,\ y_2\}$ соответственно.Найти $d$ -- расстояние между точками $A$ и $B$ через их координаты.
Решение.
Рассмотрим рисунок 4.
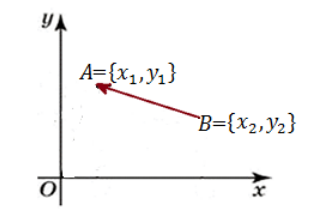
Рисунок 4. Расстояние между точками
Используя задачу 1, получим, что вектор $\overrightarrow{AB}$ имеет координаты
\[\overrightarrow{AB}=\{x_2-x_1,\ y_2-y_1\}\]Найдем длину данного вектора. По задаче 3, имеем
\[d=\left|\overrightarrow{AB}\right|=\sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2}\]Ответ: $d=\sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2}$.














