Откладывание вектора от данной точки
Для того чтобы ввести понятие умножения вектора на число, сначала необходимо разобраться в таком понятии, как откладывание вектора от данной точки.
Если точка $A$ начала какого-либо вектора $\overrightarrow{a}$, то говорят, что вектор $\overrightarrow{a}$ отложен от точки $A$ (рис. 1).

Рисунок 1. $\overrightarrow{a}$ отложенный от точки $A$
Введем следующую теорему:
От любой точки $K$ можно отложить вектор $\overrightarrow{a}$ и притом только один.
Доказательство.
Существование: Здесь нужно рассмотреть два случая:
-
Вектор $\overrightarrow{a}$ - нулевой.
В этом случае, очевидно, что искомый вектор -- вектор $\overrightarrow{KK}$.
-
Вектор $\overrightarrow{a}$ -- ненулевой.
Обозначим точкой $A$ начало вектора $\overrightarrow{a}$, а точкой $B$ - конец вектора $\overrightarrow{a}$. Проведем через точку $K$ прямую $b$ параллельную вектору $\overrightarrow{a}$. Отложим на этой прямой отрезки $\left|KL\right|=|AB|$ и $\left|KM\right|=|AB|$. Рассмотрим векторы $\overrightarrow{KL}$ и $\overrightarrow{KM}$. Из этих двух векторов искомым будет тот, который будет сонаправлен с вектором $\overrightarrow{a}$ (рис. 2)
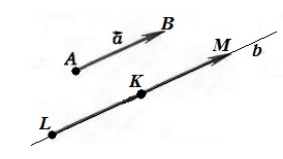
Рисунок 2. Иллюстрация теоремы 1Единственность: единственность сразу следует из построения, проведенного в пункте «существование».
Теорема доказана.
Умножение вектора на число
Пусть нам дан вектор $\overrightarrow{a\ }$ и действительное число $k$.
Произведением вектора $\overrightarrow{a\ }$ на действительное число $k$ называется вектор $\overrightarrow{b\ }$ удовлетворяющий следующим условиям:
-
Длина вектора $\overrightarrow{b\ }$ равна $\left|\overrightarrow{b\ }\right|=\left|k\right||\overrightarrow{a\ }|$;
Векторы $\overrightarrow{a\ }$ и $\overrightarrow{b\ }$ сонаправлены, при $k\ge 0$ и противоположно направлены, если $k
Обозначение: $\ \overrightarrow{b\ }=k\overrightarrow{a\ }$.
Отметим, что в результате произведения вектора на число всегда получается векторная величина.
Свойства произведения вектора на число
-
Произведение любого вектора с числом ноль равняется нулевому вектору.
Доказательство.
По определению 2, имеем $\left|\overrightarrow{b\ }\right|=\left|k\right|\left|\overrightarrow{a\ }\right|=0\cdot \left|\overrightarrow{a\ }\right|=0$, следовательно,$\overrightarrow{b\ }=k\overrightarrow{a\ }=\overrightarrow{0}$
-
Для любого вектора $\overrightarrow{a\ }$ и любого действительного числа $k$ векторы $\overrightarrow{a\ }$ и $k\overrightarrow{a\ }$ коллинеарны.
Доказательство.
Так как по определению 2, векторы $\overrightarrow{a\ }$ и $k\overrightarrow{a\ }$ сонаправлены или противоположно направлены (в зависимости от значения $k$), то они будут коллинеарны.
-
Для любых действительных чисел $m$ и $n$ и вектора $\overrightarrow{a\ }$ справедлив сочетательный закон:
\[\left(mn\right)\overrightarrow{a\ }=m(n\overrightarrow{a\ })\]Доказательство этого закона иллюстрирует рисунок 3.
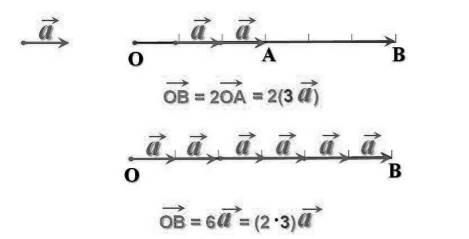
Рисунок 3. Сочетательный закон -
Для любых действительных чисел $m$ и $n$ и вектора $\overrightarrow{a\ }$ справедлив первый распределительный закон:
\[\left(m+n\right)\overrightarrow{a\ }=m\overrightarrow{a\ }+n\overrightarrow{a\ }\]Доказательство этого закона иллюстрирует рисунок 4.
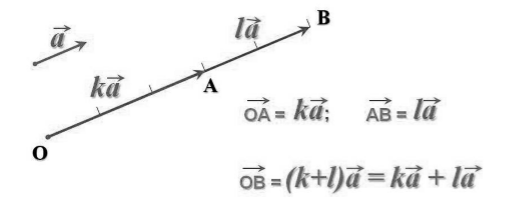
Рисунок 4. Первый распределительный закон -
Для любого действительного числа $m$ и векторов $\overrightarrow{a\ }$ и $\overrightarrow{b\ }$ справедлив второй распределительный закон:
\[m\left(\overrightarrow{a\ }+\overrightarrow{b}\right)=m\overrightarrow{a\ }+m\overrightarrow{b\ }\]Доказательство этого закона иллюстрирует рисунок 5.
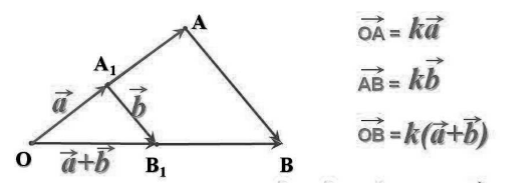
Рисунок 5. Второй распределительный закон
Пример задачи на использование понятия произведения вектора на число
Пусть $\overrightarrow{x}=\overrightarrow{a\ }+\overrightarrow{b}$, $\overrightarrow{y}=\overrightarrow{a\ }-\overrightarrow{b}$. Найти векторы:
-
$2\overrightarrow{x}+2\overrightarrow{y}$
-
$\overrightarrow{x}+\frac{1}{2}\overrightarrow{y}$
-
$-\overrightarrow{y}-\overrightarrow{x}$
Решение.
-
$2\overrightarrow{x}+2\overrightarrow{y}=2\left(\overrightarrow{a\ }+\overrightarrow{b}\right)+2\left(\overrightarrow{a\ }-\overrightarrow{b}\right)=2\overrightarrow{a\ }+2\overrightarrow{b}+2\overrightarrow{a\ }-2\overrightarrow{b}=4\overrightarrow{a\ }$
-
$\overrightarrow{x}+\frac{1}{2}\overrightarrow{y}=\overrightarrow{a\ }+\overrightarrow{b}+\frac{1}{2}\left(\overrightarrow{a\ }-\overrightarrow{b}\right)=\overrightarrow{a\ }+\overrightarrow{b}+\frac{1}{2}\overrightarrow{a\ }-\frac{1}{2}\overrightarrow{b}=\frac{3}{2}\overrightarrow{a\ }+\frac{1}{2}\overrightarrow{b}=\frac{3\overrightarrow{a\ }+\overrightarrow{b}}{2}$
-
$-\overrightarrow{y}-\overrightarrow{x}=-\left(\overrightarrow{a\ }-\overrightarrow{b}\right)-\left(\overrightarrow{a\ }+\overrightarrow{b}\right)=-\overrightarrow{a\ }+\overrightarrow{b}-\overrightarrow{a\ }-\overrightarrow{b}=-2\overrightarrow{a\ }$











