Формулы сложения
Основные формулы сложения представляют собой тригонометрические функции суммы и разности углов:
Синус, косинус и тангенс двойного угла
Синус, косинус и тангенс двойного угла представляют собой частный случай тригонометрических функций кратных углов, а также тригонометрических функций половинных углов.
Формулы кратных углов:
Формулы половинных углов:
В этих формулах перед знаком радикала должен быть поставлен знак $"+"$ или $"-"$ в зависимости от того, в какой четверти находится угол $\frac{\alpha }{2} $.
Решение прямоугольных треугольников.
Задачи на решение прямоугольных треугольников распределяются на две основные группы:
-
заданы две стороны прямоугольного треугольника; требуется определить третью сторону и оба острых угла;
-
заданы сторона и острый угол прямоугольного треугольника; требуется определить две остальные стороны и второй острый угол.
Заданы катет $a$ и гипотенуза $c$.
Задача относится к первой группе. Для определения второго катета используется теорема Пифагора: $b=\sqrt{c^{2} -a^{2} } $. Синус угла $A$: $\sin A=\frac{a}{c} $. Для вычисления значения угла $A$ используем обратную тригонометрическую функцию $A=\arcsin \frac{a}{c} $. Второй острый угол: $B=90{}^\circ -A$.
Пример решения задачи с использованием калькулятора: задано значение синуса угла $\sin A=0,5$; используя калькулятор Windows, вычислить значения угла $A$ в градусах через обратную тригонометрическую функцию.
а) Запустить калькулятор и перевести его в следующее состояние (Вид -- Инженерный, кнопка Inv -- нажата, отмечен пункт Градусы):
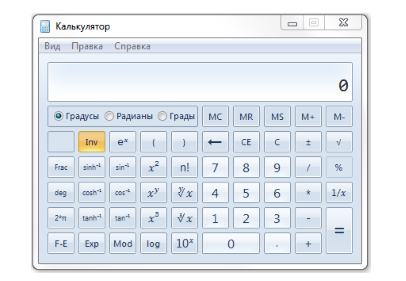
Рисунок 1.
б) Набрать число 0.5:
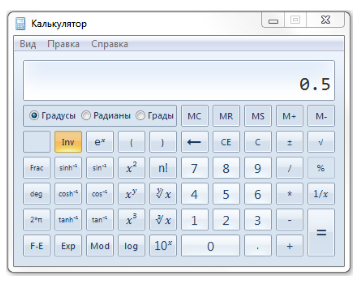
Рисунок 2.
в) Нажать кнопку

Рисунок 3. Условное обозначение функции arcsin
г) Прочитать с индикатора значение $30{}^\circ $.
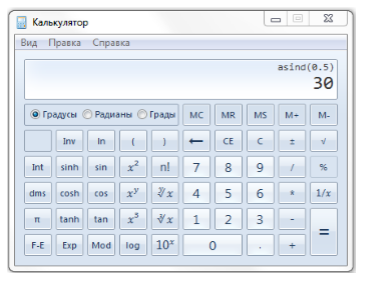
Рисунок 4.
Заданы оба катета $a$ и $b$.
Задача относится к первой группе. Для определения гипотенузы используется теорема Пифагора: $c=\sqrt{a^{2} +b^{2} } $. Тангенс угла $A$: $tgA=\frac{a}{b} $. Для вычисления значения угла $A$ используем обратную тригонометрическую функцию $A=arctg\frac{a}{b} $. Второй острый угол: $B=90{}^\circ -A$.
Заданы гипотенуза $c$ и острый угол $A$.
Задача относится ко второй группе. Второй острый угол: $B=90{}^\circ -A$. Для вычисления значения синуса и косинуса угла $A$ используем калькулятор Windows. Вычисление первого катета: $a=c\cdot \sin A$. Вычисление второго катета: $b=c\cdot \cos A$.
Заданы катет $a$ и острый угол $A$.
Задача относится ко второй группе. Второй острый угол: $B=90{}^\circ -A$. Для вычисления значения тангенса угла $B$ используем калькулятор Windows. Вычисление второго катета: $b=a\cdot tgB$. Для вычисления значения синуса угла $A$ используем калькулятор Windows. Вычисление гипотенузы: $c=\frac{a}{\sin A} $.
Для решения представленных задач могут быть использованы и другие цепочки действий. Так, например, в задаче 4 для вычисления гипотенузы можно использовать теорему Пифагора. И т.п.












